pole trapezu
pulikowski: Wyznacz pole trapezu znając długości przekątnych c,d oraz wysokość h.
24 lut 10:46
irena_1:
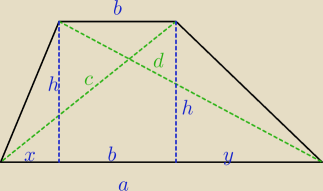
a=b+x+y
h
2+(b+y)
2=d
2
(b+y)
2=d
2−h
2
b+y=
√d2−h2
h
2+(b+x)
2=c
3
(b+x)
2=c
2−h
2
b+x=
√c2−h2
| | a+b | | b+x+y+b | | √d2−h2+√c2−h2 | |
P= |
| *h= |
| *h= |
| *h |
| | 2 | | 2 | | 2 | |
24 lut 11:18
Bogdan:
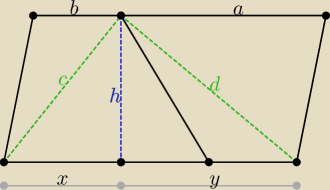
Podobnie:
| | 1 | |
x = √c2 − h2, y = √d2 − h2, pole P = |
| h(x + y) |
| | 2 | |
24 lut 11:37
pigor: ... , no to może jeszcze ja pobawię się np. tak :
szukam pola (*) P
t=
12(
a+b)h=
?, a z warunków
zadania i "mojego" rysunku (może kiedyś się "zmuszę" do
rysowania na ekranie) wyszło mi fajne równanie kwadratowe
zmiennej (
a+b), pozornie nie ciekawe:
d2=(
a+b−
√c2−h2)2+h2 ⇔ d
2= (a+b)
2−2(a+b)
√c2−h2+c
2−h
2+ h
2 ⇔
⇔ (
a+b)
2−
2√c2−h2(
a+b)+
c2−d2=0, Δ=4(c
2−h
2)−4(c
2−d
2)=
= 4(c
2−h
2−c
2+d
2)= 4(d
2−h
2) i
√Δ= 2√d2−h2 , no to tylko
a+b=
12 (2
√c2−h2+2
√d2−h2)=
√c2−h2+√d2−h2>0, stąd i z (*)
Pt= 12h (√c2−h2+ √d2−h2) − szukane
pole trapezu. ..
24 lut 13:27
pulikowski: Dziękuję wszystkim!
24 lut 13:47