log
kal:
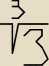
log 27
gdzie pierwiast. z trzech stopnia 3 jest podstawa a 27 wynikiem. do jakiej potegi
trzeba poniesc pierwiastek zeby uzyskac 27
dzieki za pomoc
24 lut 08:43
Janek191::
log3√3 x = 27 ?
24 lut 08:46
Janek191::
Czy log3√3 27 = x ?
24 lut 08:47
Janek191::
II wersja
x = 9
24 lut 08:48
kal: 2 wersja
ale jak to obliczyc?
24 lut 09:28
J:
= 3*log333 = 9log33 = 9
24 lut 09:29
kal: zeby to udowodnic?
24 lut 09:30
kal: rozumiem ze to √3 stopnia 3 zamieniles na 3 do potegi 3 i to wszystko tez do 3?
24 lut 09:31
J:
| | 1 | |
logamb = |
| logab ... tutaj mamy: 3√3 = 31/3 |
| | m | |
24 lut 09:34
kal: ale wtedy mnozenie dotyczy tylko 1/m* a tak? a te 27 czyli 3do 3 jest nieruszane?
24 lut 09:39
kal: ale wtedy mnozenie dotyczy tylko 1/m* a tak? a te 27 czyli 3do 3 jest nieruszane?
24 lut 09:39
J:
log3√327 = log31/327 = 3log327 = 3log333 = 9log33 = 9
24 lut 09:43
kal: czyli ta 3 wyciagnieta przed logarytm mnozy sie przez a czy przez potege ktora byla przy 3
(27+3do3) bo nie moge zrozumiec gdzie jest zasada mnozenia tego wyciagnietego wyrazu przed
logarytm przez co on sie pozniej mnozy przez ktora trojke?
24 lut 09:53
J:
| | 1 | |
popatrz na wzór 09:34 ... tutaj mamy a = 3 m = |
| stąd przed pierwiastek idzie 3,
|
| | 3 | |
24 lut 09:56
kal: tak to rozumiem tylko chodzi mi o sama koncowa faze ze ta 3 ktora stoi juz przed log to przez
co ona jest mnozona
24 lut 10:08
J:
przez drugą trójkę z wykładnika liczby logarytmowanej: logabn = nlogab
24 lut 10:13
kal: dzieki wielkie
24 lut 10:49
kal: log1/3 81√3= ?
czy to bedzie tak: = −4?
bo log1/3 (81*31/3 ) = log 1/3 (34*31/3)=log 1/3 34= (1/3 zamieniam na 34 przez
wstawinie minusa )
24 lut 11:27
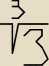 log 27
gdzie pierwiast. z trzech stopnia 3 jest podstawa a 27 wynikiem. do jakiej potegi
trzeba poniesc pierwiastek zeby uzyskac 27
dzieki za pomoc
log 27
gdzie pierwiast. z trzech stopnia 3 jest podstawa a 27 wynikiem. do jakiej potegi
trzeba poniesc pierwiastek zeby uzyskac 27
dzieki za pomoc