jak obliczyć
Michał: Z punktu P= (−1, 0) poprowadzono sieczną i styczną do okręgu o środku w sunkcie S = ( 1, √6)
Sieczna odległa jest od środka okręgu o 1 i przecina go w punktach B, oraz D Punkt A jest
punktem wspólnym okręgu i stycznej. Wiedząc że odcinek AB jest średnicą okręgu wyznacz
równanie okręgu
o; (x−1)2 + (y −√6)2 = r2
IPAI2 = IPDI*IPKI
obliczyłem
ISPI = √10 i z tw Pit z ΔPSK IPKI2 = 11 ⇒ IPK I= √11
K ∊IPBI i ISK I ⊥ I PB I i ISK I = 1
dalej nie mam pomyślu jak obliczyć r
24 lut 08:29
Janek191::
Może trzeba skorzystać z tw. o odcinkach siecznej i stycznej
Patrz po lewej stronie na:
geometria na płaszczyźnie
24 lut 08:45
Michał: IPB − sieczna IPAI − styczna
tw o odcinkach siecznej i stycznej
IPAI2 = IPDI * IPBI ale z tu mam następujące niewiadome IPAI , IPDI , IPBI
24 lut 19:00
Michał: ponawiam prośbę czy ktoś ma pomysł jak obliczyć r
25 lut 16:17
Michał: korzystają z tw oodcinkach siecznej i stycznej obliczyłem
IPAI2 = IPSI2 − ISAI2 = 10 − r2
ale nadal mam za dużo niewiadomych
a wynik jest że są dwa okręgi (x−1)2 + (y−√6)2 = 5 lub (x−1)2 + (y−√6)2= 2
25 lut 21:59
prosta: |PK| =√9=3
x− połowa długości cięciwy, y=|PA|
(3−x)(3+x)=y2 −−−−−> z tw. o odcinkach stycznej i siecznej
y2=22+(3−x)2 −−−−−>tw. Pitagorasa w ΔAPD
9−x2=4+9−6x+x2
x2−3x+2=0
x=1 lub x=2
r=√2 lub r=√5
25 lut 23:16
Michał: jak obliczyłaś że I PK I = 3 proszę o rysunek który odcinek to x a który y
25 lut 23:39
prosta: z tw. Pitagorasa w trójkącie PSK:
|PK|2+|SK|2=|PS|2
|PK|2+1=10
|PK|=3
26 lut 08:45
prosta: z tw. o stycznej i siecznej:
|PD|*|PD|=|PA|2
(3−x)(3+x)=y2 , gdzie x=0,5|BD|=|KD|=|KA|
26 lut 08:47
Michał: mam narysowany rysunek i jezeli oznaczenia twoje przeniosłem na mój to
KD ≠ KA bo z Δ PKA PK = PD + DK a PA to prosta styczna do okręgu czyli PA i KA to
ramiona Δ PKA PK to jego podstawa
26 lut 09:05
prosta: sorki
x=0,5|BD|=|KD|=|KB|
26 lut 09:27
prosta: K jest środkiem cięciwy BD
A jest punktem styczności
26 lut 09:28
Michał: jeszcze mam pytanie
na jakiej podstawie DK = 2
26 lut 09:59
5-latek: Czesc
prosta 
Dlaczego zmienilas nick?
26 lut 10:44
Michał: już wiem AD = 2 * KS − tw o odcinku łączący środki dwóch boków trójkąta Δ ADB
dziękuję bardzo
26 lut 16:18
prosta: Cześć. [P[5−latek]

to mój pierwszy i jedyny nick na tym forum

26 lut 17:31
Mila:
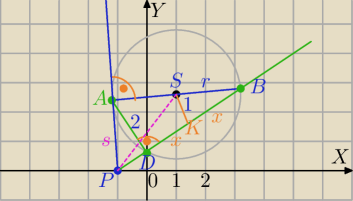
Uporządkowałam Wasze rozwiązanie.
S=(1,
√6)
P=(−1,0)
|PS|
2=2
2+
√62=10
WΔSKB:
(*) r2=x2+1
W ΔPKS:
|PS|
2=PK
2+1
2
10=|PK|
2+1
|PK|=3
Z tw. o odcinkach siecznej:
|PD|*PB|=|PA|
2, |PD|=3−x
(3−x)*(3+x)=|PA|
2
W ΔADP:
|PA|
2=2
2+(3−x)
2
(3−x)*(3+x)=4+(3−x)
2
9−x
2=4+9−6x+x
2
x
2−3x+2=0
Δ=9−8=1
x=1 lub x=2
Po podstawieniu do równania (*)
r=
√2 lub r=
√5
26 lut 22:09
Michał: jeszcze raz dziękuję wszystkim
27 lut 00:04
Mila:
Nie wiem, czy to przydało się, ale zadanie ciekawe.
27 lut 16:46
prosta: rysunek to geogebra czy geonext?
27 lut 17:16
 Dlaczego zmienilas nick?
Dlaczego zmienilas nick?
 to mój pierwszy i jedyny nick na tym forum
to mój pierwszy i jedyny nick na tym forum 
 Uporządkowałam Wasze rozwiązanie.
S=(1,√6)
P=(−1,0)
|PS|2=22+√62=10
WΔSKB:
(*) r2=x2+1
W ΔPKS:
|PS|2=PK2+12
10=|PK|2+1
|PK|=3
Z tw. o odcinkach siecznej:
|PD|*PB|=|PA|2, |PD|=3−x
(3−x)*(3+x)=|PA|2
W ΔADP:
|PA|2=22+(3−x)2
(3−x)*(3+x)=4+(3−x)2
9−x2=4+9−6x+x2
x2−3x+2=0
Δ=9−8=1
x=1 lub x=2
Po podstawieniu do równania (*)
r=√2 lub r=√5
Uporządkowałam Wasze rozwiązanie.
S=(1,√6)
P=(−1,0)
|PS|2=22+√62=10
WΔSKB:
(*) r2=x2+1
W ΔPKS:
|PS|2=PK2+12
10=|PK|2+1
|PK|=3
Z tw. o odcinkach siecznej:
|PD|*PB|=|PA|2, |PD|=3−x
(3−x)*(3+x)=|PA|2
W ΔADP:
|PA|2=22+(3−x)2
(3−x)*(3+x)=4+(3−x)2
9−x2=4+9−6x+x2
x2−3x+2=0
Δ=9−8=1
x=1 lub x=2
Po podstawieniu do równania (*)
r=√2 lub r=√5