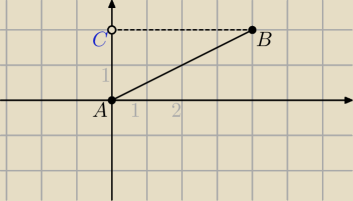
analityczna Zuzka: Proszę o sprawdzenie Wyznacz na osi OY taki punkt C, aby trójkąt o wierzchołkach A(0,0), B(4,2) i C był trójkątem prostokątnym. Rozpatrz dwa przypadki. AB= √20 BC = √y²+4y+20 AC=√y²+2y 1) y= −20 2) y1= −3 y2=0

Zuzka: pomoże ktoś?

Janek191:: 1) C = ( 0 ; 2)

Metis:

Janek191:: 2) C = ( 0 ; 10)

Zuzka: tak, ale z obliczen tak nie wychodzi

Zuzka: 1) AC²=AB²+BC² i wychodzi y = −20 2) AB²=BC²+AC²

Janek191:: Wychodzi: C = ( 0; y) A = ( 0; 0) B = ( 4; 2) więc I A B I² = 4² + 2² = 20 I AC I² = y² I BC I² = ( (0 − 4)² + ( y − 2)² = 16 + y² − 4y + 4 = 20 + y² − 4y Z tw. Pitagorasa: I AB I² + I BC I² =I AC I² czyli 20 + 20 + y² − 4 y = y² 40 = 4 y y = 10 C = ( 0 , 10) =========

Janek191:: I gdzie ta Zuzka ?

Zuzka: faktycznie, wkradł się jeden błąd rachunkowy wcześniej, dzięki za sprawdzenie