Ile wielomian ma pierwiastków? luk: Dany jest wielomian W(x)=x³ − 4√2*x² + 10x − 4√2 1) Ile rożnych pierwiastków ma ten wielomian?

Janek191:: W'(x) = 3 x² − 8√2 x + 10 Δ = 128 − 4*3*10 = 128 − 120 = 8 √Δ = 2√2

	8√2 − 2√2
x1 =		= √2
	6

	8√2 + 2√2		5
x2 =		=		√2
	6		3

oraz W ''( x) = 6 x − 8√2 więc W ''( x₁) < 0 − funkcja ( wielomian W ) ma maksimum lokalne W_max = (√2)³ − 4√2*2 + 10√2 − 4√2 = 2√2 − 8√2 + 6√2 = 0 i

	5
W '' ( x2) = 6*		√2 − 8√2 = 10√2 − 8√2 = 2√2 > 0 − wielomian W ma
	3

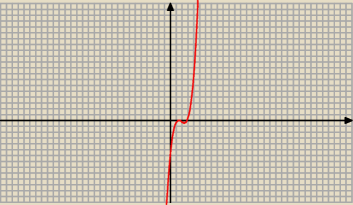
minimum lokalne W_min < 0 Odp. Ten wielomian ma dwa różne pierwiastki.

Gray: Można i tak: ponieważ W(√2}=W'(√2)=0 oraz W"(√2)≠0 zatem W ma dwa różne pierwiastki rzeczywiste (jeden podwójny).