całki podwójne bezendu: Obliczyć całkę funkcji ƒ(x,y)=x+y w obszarze ograniczonym krzywymi y=x²+2 oraz y=2x².

	64√2
Mój wynik to
	15

Potwierdzi ktoś ?

bezendu: Mila ?

Krzysiek: ∫−√2√2∫2x2x2+2(x+y)dydx Tylko coś mi wolfram nie chce się załadować

bezendu: Dzięki

Krzysiek: Tyle samo wyliczyło.

Mila: Zgadza się.

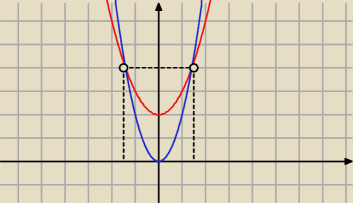
Dziadek Mróz: f(x) = x² + 2 g(x) = 2x² f(x) = g(x) x² + 2 = 2x² −x² = −2 x² = 2 x = ±√2 y₂ = g(√2) = 2(√2)² = 2*2 = 4

	−Δ
y1 = qg(x) =		= ... = 0
	4a

₀∫⁴(_−√2∫^√2(x + y)dx)dy = *) _−√2∫^√2(x + y)dx = _−√2∫^√2xdx + y_−√2∫^√2dx =

	x2		(√2)2		(−√2)2
= [		+ yx]−√2|√2 =		−		+ √2y + √2y =
	2		2		2

	2		2
=		−		+ 2√2y = 2√2y
	2		2

	y2
*) = 0∫42√2ydy = 2√20∫4ydy = 2√2[		]0|4 =
	2

	42		02
= 2√2[		−		] = 2√2[8 − 0] = 16√2
	2		2

bezendu: Dziękuję

Dziadek Mróz: A to mam źle