Planimetria xyz: 1. Kąt przy podstawie trapezu równoramiennego ma miarę 30 stopni. Dłuższa podstawa jest równa 6√3, a ramię ma długość 3. Oblicz promień okręgu opisanego na tym trapezie. Obliczyłam że przekątna jest równa 3√7 i taka jest odpowiedź ale nie rozumiem czemu przekątna to jednocześnie promień okręgu opisanego na nim. 2. Wysokości równoległoboku wynoszą 2,4cm i 4cm a jego obwód jest równy 16cm Oblicz cosinus kąta rozwartego między przekątnymi tego równoległoboku

	6		6
Wyliczyłam boku : 3 i 5 następnie z jedynki trygonometrycznej cosα=		lub cosα=−
	10		10

Dalej nie mam pomysłu co

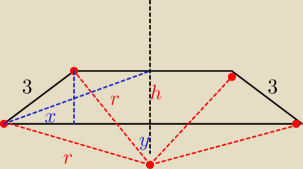Janek191:: Mamy a = 6√3

h
	= sin 30o ⇒ h = 1,5
3

x		√3
	= cos 30o =		⇒ x =1,5 p{3]
3		2

b = a − 2 x = 3√3 0,5 b = 1,5√3 r² = (0,5 b)² + ( h + y)² = 2,25*3 + ( 1,5 + y)² = 6,75 + ( 1,5 + y)² oraz r² = (0,5 a)² + y² = ( 3 √3)² + y² = 27 + y² więc 6,75 + (1,5 + y)² = 27 + y² 6,75 + 2,25 + 3y + y² = 27 + y² 3 y = 27 − 9 = 18 y = 6 ==== zatem r² = ( 3√3)² + y² = 9*3 + 36 = 27 + 36 = 63 r = √63 = p{9*7) = 3√7 ===================

prosta: Zad.2

	3
α− kąt ostry równoległoboku , więc cosα=
	5

	3
β− kąt rozwarty cosβ=cos(180o−α)=−cosα=−
	5

prosta: dalej policzyć przekątne i z tw. cosinusów kąt między nimi

xyz:

	3
A czemu bierzemy pod uwagę cosα		a ten drugi odrzucamy ?
	5