rownanie olk: Rozwiaz rownanie:−2sin²x−cosx+1=0 i x nalezy <0,2π>

Janek191:: 1 − 2 sin² x = cos 2 x cos 2 x − cos x = 0 2 sin{1,5x} sin (− 0,5 x) = 0 − 2 sin (1,5 x)*sin 0,5 x = 0 sin 1,5 x = 0 lub sin 0,5 x = 0 itd.

olk: Itd?

Janek191:: I tak dalej − tzn. dokończ

olk: ale mozesz to w calosci zapisac, bo bladego pojecia nie mam o co w tym chodzi

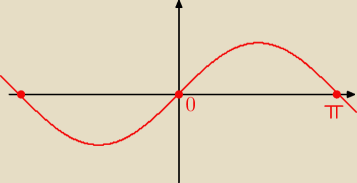
Janek191:: cd. Z wykresu funkcji sinus mamy : sin 1,5 x = 0 ⇔ 1,5 x = k*π lub sin 0,5 x = 0 ⇔ 0,5 x = k*π więc

	2
x =		π* k lub x = 2π*k , gdzie k − dowolna liczba całkowita
	3

Janek191::