w trapezie abcd (ab II cd) IABI>ICDI przekatne przecinaja sie w punkcie E. Pol dyzio073: w trapezie abcd (ab II cd) IABI>ICDI przekatne przecinaja sie w punkcie E. Pole trójkąta DEC=12 P trojkata DEA = 16 oblicz pole trapezu.

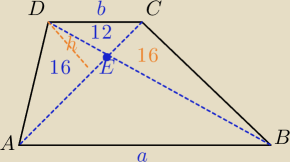
Mila: P_ΔDEA=P_ΔBEC =16 ΔDEA i ΔDEC mają wspólną wysokość ⇔

EC		12		3
	=		=
EA		16		4

⇔

PΔCEB		3
	=		⇔
PΔAEB		4

16		3
	=
PΔAEB		4

	64
PΔAEB=
	3

	64
PABCD=2*16+12+
	3

===================

dyzio073: a nie mozna zrobic tak ze 12+12+16+16?

Mila: Przecież nie dwóch Δ o polu 12. Przeczytaj dokładnie co napisałam.

dyzio073: oooo dziękuję już wiem w trapezie abcd (ab II cd) IABI>ICDI przekatne przecinaja sie w punkcie E. Pole trójkąta AED=18 P trojkata DEC = 10 oblicz pole trapezu? A takie jak zrobic?

Mila: Tak samo . Wzoruj się na moim rozwiązaniu i napisz ostatnie działanie.

dyzio073: ¹⁸_PΔAEB=¹⁰₁₈ → 324=10PΔAEB PΔAEB=32,4

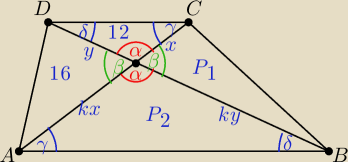Bogdan: Inny sposób: Trójkąty ABE i CDE są podobne w skali k i β = 180^o − α ⇒ sinβ = sinα

1		1		4
	xysinα = 12,		kx*ysinα = 16 ⇒ 12k = 16 ⇒ k =		,
2		2		3

	1		1		4		64
P1 =		x*kysinα = 16, P2 =		*kx*kysinα =		*16 =
	2		2		3		3

Pole trapezu P = 12 + 16 + P₁ + P₂

Mila: Dobrze.

	10		5
k=		=		skala podobieństwa ΔDEC do ΔABE
	18		9

Można jeszcze tak:

PΔDEC
	=k2⇔
PΔABE

10		25
	=
x		81

	810
x=
	25

x=P_ΔABE=32,4

dyzio073: jejku dziękuję wam

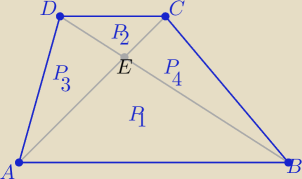Eta: No to jeszcze tak P₃=P₄ i P₃=k*P₂ , k −− skala podobieństwa trójkątów ABE i DEC

	16		4
stąd k=		=
	12		3

	7
P(trapezu)= (k+1)2*P2 ⇒ P=(		)2*12=........
	3

bezendu: Wystarczy wpisać w wyszukiwarkę Trapez−Eta. Masz milion zadań rozwiązanych krok po kroku z rysunkami

Eta: ?

bezendu: To po środku