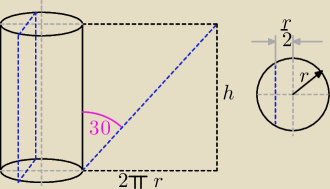
Bryły Dżepetto 18: Powierzchnia boczna walca jest prostokątem, którego przekątna tworzy z bokiem przystającym do

	1
wysokości kąt o mierze 30'. Płaszczyzna równoległa do osi walca i oddalona od niej o		r
	2

promienia podstawy podzieliła walec na obie bryły. Wyznacz stosunek ich objętości. Odpowiedzi:

	πr3√3(4π−3√3)		πr3√3(8π+3√3)
V1 =		oraz V2 =
	6		6

Z góry dzięki za wytłumaczenie zadanka

dero2005:

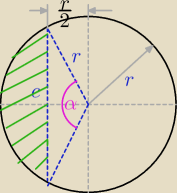
dero2005: liczę długość cięciwy c

c		√3
	= √r2−(r2)2 =		r
2		2

c = r√3 liczę kąt α c² = 2r² − 2r²cosα ⇒ wzór cosinusów 3r² = 2r² − 2r²cosα

	1
cosα = −
	2

α = 120^o liczę pole wycinka koła o promieniu r i kącie 120^o

	120		πr2
Pw =		*πr2 =
	360		3

licze pole trójkąta c,r,r

	c*r2		√3
Pt =		=		r2
	2		4

liczę pole odcinka koła (zielone zakreskowanie) jako różnicę pola wycinka koła i pola trójkąta

	r2
Po= Pw − Pt =		(4π−3√3)
	12

liczę wysokość h walca

2πr		√3
	= tg30o =
h		3

h = 2πr√3 liczę pole większej części koła

	r2
Pk = πr2 − Po =		(8π + 3√3)
	12

	πr3√3
Vo = Po*h =		(4π−3√3)
	6

	πr3√3
Vk = Pk*h =		(8π+3√3)
	6

dokończ dalej

Dżepetto 18: Świetna pomoc! Doceniam trud i prostotę przekazu z jaką pomogłeś mi z tym zadaniem. Jeszcze raz bardzo dziękuję za profesjonalne podejście do pomocy!