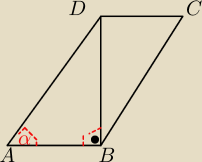
Obwody,pole powierzchni, obrót wokół boku. Serum: Kat przy wierzchołku A równoległoboku ABCD jest równy α, a krótsza przekatna jest prostopadła do boków AB i CD. Objętość bryły powstałej przez obrót równoległoboku wokół boku AB jest równa V. Wyznacz pole powierzchni tej bryły. Nie mogę sobie tego wyobrazić ; D

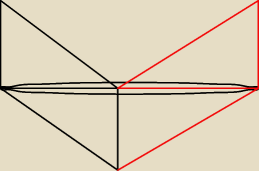Kacper: Jak skleimy dwie bryły to dostaniemy szukaną

pigor: ..., ja ci tego ... nie narysuję, ale opisze np. tak : w ΔABD,

	H
niech |AD|=l=		, |AB|=H , |BD|=r=H tgα − zgodnie ze standardowymi
	cosα

oznaczeniami w stożku, to po obrocie zgodnie z zadaniem powstanie bryła, o objętości : V_bryły= V_{stożka ADD} + V_{walca DD' CC '} − V_{stożka CBC '} = = V_{walca DD 'CC '}, bo te 2 stożki we wzorze są identyczne i redukują się, czyli przy oznaczeniach długości powyżej mamy równanie: V_{walca DD 'CC '}= V_bryły ⇔ πr²H=V ⇒ πH³tg²α=V ⇔ ⇔ (*) H³= ¹_πctg²α , zatem P_c.bryły= 2P_b.stożka+P_b.walca= 2πr l+2πr H= 2πr (l+H)=

	H		1
= 2π H tgα (		+H)= 2π H2(		+1)=
	cosα		cosα

	1+cosα
= 2π3√ 1πctg2α 2 *		=
	cosα

	1+cosα		1+cosα
= 2π*1π3√π2ctgα* ctgα*		= 23√π2ctgα*		=
	cosα		sinα

	2cos212α
= 23√π2ctgα*		= 2 ctg12α 3√π2 ctgα.
	2sin12αcos12α

pigor: .., o masz rysunek.. niedokończony, bo brakuje mu podstawy (koła) od górywspólnego dla walca i stożka identycznego temu na dole ale "wcinającego się" od góry bryły w walec, (te 2 stożki i walec mają tej samej długości wysokości H i promienie r podstaw). ...

Serum: WOW, dzięki wszystkim za pomoc