rachuneczeq geometrykz: dość rozbudowane zadanie z rachunku: W pierwszej urnie są tylko kule czarne i białe, w drugiej urnie jest 6 kul niebieskich i 4 zielone, a w trzeciej urnie są 2 kule niebieskie i 8 zielonych. Losujemy jedną kulę z pierwszej urny. Jeżeli wylosowana kula jest czarna, to losujemy jedną kulę z drugiej urny, a jeżeli biała, to losujemy jedną kulę z trzeciej urny. Prawdopodobieństwo wylosowania kuli zielonej jest dwa razy większe od prawdopodobieństwa wylosowania kuli niebieskiej. Oblicz prawdopodobieństwo wylosowania z pierwszej urny kuli czarnej. hmm? mnie przerasta

Frost: I URNA II URNA III URNA n czarnych m białych 6 N 4 Z 2N 8Z

	n
P(A)− Prawdopodobieństwo wylosowania kuli czarnej z I urny P(A)=
	n+m

	m
P(B)− Prawdopodobieństwo wylosowania kuli białej z I urny P(B)=
	n+m

	4
P(C1)− prawdopodobieństwo wylosowania kuli zielonej z II urny P(C1)=
	10

	8
P(C2)− prawdopodobieństwo wylosowania kuli zielonej z III urny P(C2)=
	10

	6
P(D1)− prawdopodobieństwo wylosowania kuli niebieskiej z II urny P(D1)=
	10

	2
P(D2)− prawdopodobieństwo wylosowania kuli niebieskiej z III urny P(D2)=
	10

P(E) −prawdopodobieństwo wylosowania kuli zielonej

	n		4		m		8		2n+4m
P(E)=		*		+		*		=
	n+m		10		n+m		10		5(n+m)

P(F)− prawdopodobieństwo wylosowania kuli niebieskiej

	n		6		m		2		3n+m
P(F)=		*		+		*		=
	n+m		10		n+m		10		5(n+m)

P(E)=2P(F)

2n+4m		3n+m
	=2*
5(n+m)		5(n+m)

2n+4m=6n+2m 4n=2m m=2n

	n
P(A)=
	n+m

	n
P(A)=
	n+2n

	1
P(A)=
	3

geometrykz: dzięki wielkie, teraz wszystko jasne. sam bym pewno na to nigdy nie wpadł. najgorszy dział na maturze już wolę planimetrię. jak się cholerstwo trafi i nie będę umiał to po maturze, bo pewno 4−6 pkt będzie za to cholerstwo dzięki jeszcze raz.

Frost: Właśnie prawdopodobieństwo to dla mnie na maturze będą darmowe punkty Na pewno na rozszerzeniu będzie kombinatoryka albo prawdopodobieństwo

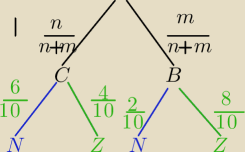
Mila: nC, mB 6N,4Z 2N,8Z P(Z)=2*P(N) Potrafisz zliczyć z drzewka?

geometrykz: o, teraz łatwiej, zamknąłem tamto rozwiązanie i zacząłem robić drzewkiem, i udało się, ale to pewno dlatego, że pamiętałem co i jak zrobić @Frost, ja lubię kombinatorykę. Zadania typu "ile jest liczb..." to moje ulubione, ale prawdopodobieństwo mi kiepsko idzie, a nie mogę nawet jednego zadania na maturze ominąć, lipa dlatego muszę katować to prawdopodobieństwo, aż mi wejdzie i pojmę to dostatecznie. w szkole jestem w połowie dopiero, wątpię żeby moja klasa się wyrobiła ze stereometrią do matury..

Frost: Ja właśnie zacząłem stereometrie. Z prawdopodobieństwa miałem sprawdzian w środę 5+ Będzie dobrze PS. Miałem Ci rysować drzewko ale nie lubię tego robić tutaj

Mila: Znacznie łatwiej, bo masz przed sobą schemat przebiegu doświadczenia losowego.

geometrykz: ale na szczęście doświadczenie losowe w szkole jeszcze przede mną, mam nadzieję, że pojmę.

geometrykz: podepnę w takim razie. dlaczego zadania: W urnie są 3 kule białe, 4 czarne i 5 zielonych. Losujemy ze zwracaniem 3 kule. Oblicz prawdopodobieństwo tego, że wśród wylosowanych kul będą: biała i czarna. Czyli możliwości:

	3		3		4		3!
biała, biała, czarna;		*		*		*
	12		12		12		2!

	3		4		4		3!
biała, czarna, czarna;		*		*		*
	12		12		12		2!

	3		4		5
biała, czarna,zielona;		*		*		* 3!
	12		12		12

(czy kolejność jest ważna? jeśli tak to dlaczego − jeśli nie − dlaczego?) robię za pomocą drzewka i mi źle wychodzi... o około 0,00006...

geometrykz: dobra − już mi wyszło. tylko sam nie wiem dlaczego kolejność ma znaczenie, mimo że to moje rozwiązanie..

geometrykz: zawsze jeśli losuję ze zwracaniem, to kolejność ma znaczenie, tak? pytania typowo podstawowe, ale co ja poradzę..

żyd: ale po co Ci te silnie potrzebne ?

geometrykz: bo mogę wylosować BBC, BCB, CBB BCC CCB CBC BCZ BZC ZCB ZBC CBZ CZB czyż nie?

zyd: to nie ma znaczenia ważne żebyś wylosował bbc a w jakiej kolejności to już Cie to nie interesuje

geometrykz: ale wtedy będzie niepoprawnie, a mój wynik pasuje do odpowiedzi. http://www.medianauka.pl/kombinatoryka_prawdopodobienstwo tutaj znalazłem, że "losowanie ze zwracaniem" − liczy się kolejność?

geometrykz: to jak to będzie w końcu x(

zyd: ze zwracaniem będziesz miał inne współczyniki w mianowniku tzn 12, 11 ,10. nie nie liczy się w poleceniu przeważnie bedziesz mial zaznaczone ze 1 kula to kula białą itp

zyd: bez zwracania*

geometrykz: jak to? a jeśli mam 10 kul: 5 białych i 5 niebieskich w jednej urnie.

	5		5		5		4
Szansa na dwie białe to:		*		, a nie		*		, bo w końcu ze
	10		10		10		9

zwracaniem, czyli biorę i zwracam, mam tę samą ilość kul, jaką miałem przed sięganiem do urny.

geometrykz: dobra, rozumiem. ale my ciągle rozmawiamy o przypadku ze zwracaniem, tamto zadanie miało w treści " Losujemy ze zwracaniem 3 kule".