geometria-zadanie
Magda: Dany jest trójkąt ABC. Udowodnij, że dwusieczna kąta A trójkąta, symetralna boku BC i okrąg
opisany na trójkącie mają punkt wspólny.
23 lut 12:13
===:
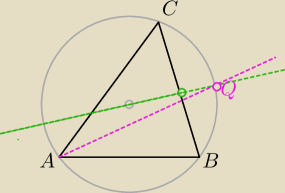
dowód jest banalny jak przeanalizujesz łuki BQ i CQ
23 lut 12:25
Magda: Są równej długości?
23 lut 13:14
===:
a są ... tylko powiedz dlaczego?
23 lut 13:32
Magda: Bo na tych łukach oparte są kąty o takich samych miarach.
23 lut 13:53
===:
i wszystko jasne
Teraz tylko "ubrać" cały dowód−

23 lut 13:59
Magda: A co ma do tego symetralna?
23 lut 14:56
===:
... a narysowałem Ci.
Środek okręgu wyznaczają

?
23 lut 15:04
Magda: Punkt przecięcia symetralnych trójkąta.
23 lut 15:05
===:
Czyli symetralna przechodząc przez środek okręgu i środek odcinka BC dzieli łuk BC na
połowy.
Skoro dwusieczna kąta A też dzieli łuk na BC na połowy to również przechodzi przez Q
... jest więc Q punktem wspólnym okręgu dwusiecznej i symetralnej
23 lut 15:09
Magda: Dziękuję.
23 lut 15:10
pigor: ... , symetralna odcinka
jest miejscem geometrycznym punktów równo oddalonych
od końców odcinka tu AB (cięciwy 'spinającej' łuk AB=QA U QB)
a więc między innymi punktu Q takiego, że |QC|=|QB| . ...

23 lut 15:13
 dowód jest banalny jak przeanalizujesz łuki BQ i CQ
dowód jest banalny jak przeanalizujesz łuki BQ i CQ

 ?
?
