22 lut 23:47
bezendu:
Qulka Ty to zdjęcie kalkulatorem robiłaś ?
22 lut 23:49
Qulka: wiem wiem..widziałam dziś aplikację w telefonie co jak się najedzie na wzór równania to je
rozwiązuje
niezły bajer
ale ja się przywiązuję do rzeczy i dopóki mi nie padnie całkiem to mój archaiczny telefonik mi
wystarcza
22 lut 23:53
lel: podasz nazwę aplikacji
?
22 lut 23:59
jakubs: photomath coś takiego widziałem kiedyś w sieci
23 lut 00:00
Saris: Nie wierzę, żeby to coś rozwiązywało coś bardziej złożonego.
23 lut 00:01
Prosiak: łiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
iiiiiiiiiiiiiiiiiiiiiiiiiiii
23 lut 00:02
Qulka: na razie miało kłopoty, ale wierzę w naszych programistów
dopracuje się szybko
23 lut 00:03
jakubs: Saris wystarczy, żeby aplikacja dobrze rozpoznawała, a z resztą nie będzie problemu
23 lut 00:12
Qulka: a co z moim czworościanem
23 lut 00:12
Saris: hehe, nie będzie? To wlasnie mysle ze mniejszy problem jest z algorytmem zczytującym i
rozpoznającym problem niż tym, który go rozwiąże.
23 lut 00:14
mysia pysia: kulko ja nie mam pojecia nie rozumiem nawet treści zadania więc Ci nie pomogę
23 lut 00:14
Daansa: Miejsce styku plaszczyzny z wysokoscia
aleee to juz pewnie wiesz
23 lut 00:21
Qulka: ale w odpowiedziach była jakaś liczba, i jako wskazówkę kazali rozważyć płaszczyznę zwierającą
wysokość postawy i wysokość ostrosłupa ... a mi wychodzi zero
nawet model z geomagów nie
pomógł
23 lut 00:36
Hugo: Hugo programista dopracuje
23 lut 00:56
Daansa:
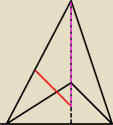
chyba tak
kurczaki musze sie zastanowic
23 lut 02:05
===:
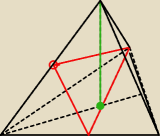
a co tu jest do liczenia
?
23 lut 11:44
Qulka: no właśnie.. a w odpowiedziach jest wynik zdecydowanie różny od zera
23 lut 11:51
===:
bo pewnie jest błąd w treści zadania.
Płaszczyznę pewnie poprowadzono przez krawędź podstawy (a nie wysokość) i środek
krawędzi bocznej nie mającej wierzchołka z tą krawędzią podstawy
23 lut 12:01
Dziadek Mróz:
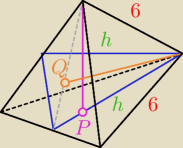
Z tego co czytam i rozumiem odległość to 0
O ile rzucamy inną wysokość ostrosłupa (Q).
23 lut 12:02
===:
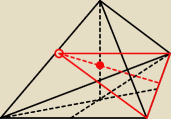
23 lut 12:06
Qulka: przez krawędź podstawy było zadanie wcześniej więc raczej nie jest to właściwa poprawka
23 lut 12:20
===:
Możliwy błąd przy składaniu.
Sama widzisz, że jeśli jak w treści to wysokość ostrosłupa przebija płaszczyznę przekroju
na wysokości podstawy czyli na płaszczyźnie podstawy
23 lut 12:30
Qulka: bałam się że może jednak czegoś nie widzę
zwłaszcza że w odpowiedziach jeszcze podali
wskazówkę i książka ma któreś wydanie, więc raczej błędy w niej wyłapano
bo niektóre świeżynki maja takie kwiatki, że aż się miło czyta
(czasem widać jak ekspresowo
na potrzeby zmian powstawały
)
23 lut 12:35
===:
−
23 lut 12:52