zespolone
wita:
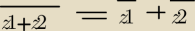
cześć, treśc zadania :
Wykazać, że dla dowolnych liczb zespolonych z1,z2 zachodzi (rysunek).
W zbiorze liczb zespolonych rozwiązać równanie. Wynik sprawdzić.
(1+i)z
2−(6+4i)z+17+19i=0
Dochodzę do czegoś takiego, pytanie brzmi czy dobrze i co dalej:
(6+4i)−4(1+i)(17+19i)=0
36+48i+16i
2−4(17+19i+17i+19i
2)
36+48i+16i
2−68−76i−68i−76i
2
delta= 28−96i
22 lut 22:06
Janek191::
z1 = a + b i
z2 = c + d i
więc
z1 + z2 = ( a + c) + ( b + d) i
zatem
−−−−−
z1 + z2 = ( a + c) − ( b + d) i
oraz
−
z1 = a − b i
−
z2 = c − d i
więc
− −
z1 + z2 = ( a − b i) + ( c − d i) = (a + c) − ( b + d) i
L = P
ckd.
23 lut 08:30
Janek191::
( 1 + i) z
2 − ( 6 + 4 i) z + 17 + 19 i = 0
Δ = ( 6 + 4 i)
2 − 4*( 1 + i)*( 17 + 19 i) = 36 + 48 i + 16 i
2 − ( 4 + 4 i )*( 17 + 19 i) =
= 36 + 48 i − 16 − ( 68 + 76 i + 68 i +76 i
2) = 20 + 48 i − ( 68 + 144 i − 76) =
= 20 + 48 i + 8 − 144 i = 28 − 96 i = 4*( 7 − 24 i ) = 4*( 4 − 3 i)
2
więc
√Δ =
√ 4*( 4 − 3 i)2 = 2*( 4 − 3 i) = 8 − 6 i
więc
| | 6 + 4 i − 8 + 6 i | | − 2 + 10 i | | − 1 + 5 i | |
z1 = |
| = |
| = |
| = |
| | 2 + 2 i | | 2 + 2 i | | 1 + i | |
| | ( − 1 + 5 i )*( 1 − i) | | − 1 + i + 5 i − 5 i2 | |
= |
| = |
| = |
| | ( 1 + i )*( 1 − i) | | 1 − i2 | |
z
2 = ... dokończ

23 lut 08:56
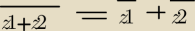 cześć, treśc zadania :
Wykazać, że dla dowolnych liczb zespolonych z1,z2 zachodzi (rysunek).
W zbiorze liczb zespolonych rozwiązać równanie. Wynik sprawdzić.
(1+i)z2−(6+4i)z+17+19i=0
Dochodzę do czegoś takiego, pytanie brzmi czy dobrze i co dalej:
(6+4i)−4(1+i)(17+19i)=0
36+48i+16i2−4(17+19i+17i+19i2)
36+48i+16i2−68−76i−68i−76i2
delta= 28−96i
cześć, treśc zadania :
Wykazać, że dla dowolnych liczb zespolonych z1,z2 zachodzi (rysunek).
W zbiorze liczb zespolonych rozwiązać równanie. Wynik sprawdzić.
(1+i)z2−(6+4i)z+17+19i=0
Dochodzę do czegoś takiego, pytanie brzmi czy dobrze i co dalej:
(6+4i)−4(1+i)(17+19i)=0
36+48i+16i2−4(17+19i+17i+19i2)
36+48i+16i2−68−76i−68i−76i2
delta= 28−96i
