funkcja kwadratowa erw: Jednym z miejsc zerowych funkcji kwadratowej jest liczba 5, maksymalny przedział w którym ta funkcja jest malejąca to <2;+∞). Największa wartość funkcji w przedziale <−8;−7> jest równa −24. Wyznacz wzór funkcji i narysuj jej wykres. Mógłby mi ktoś powiedzieć jak krok po kroku rozwiązać to zadanie?

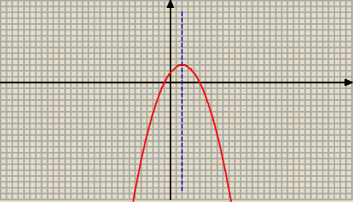
Janek191:: a < 0 x₂ = 5 p = 2 więc

	x1 + x2
p =
	2

	x1 + 5
2 =
	2

4 = 5 + x₁ x₁ = − 1 f( − 7) = − 24 f(x) = a*( x − x₁)*( x − x₂) = a*(x + 1)*( x − 5) oraz

	1
f( − 7) = a*( − 7 + 1)*( − 7 − 5) = a*( − 6)*( − 12) = 72 a = − 24 ⇒ a = −
	3

	1
Odp. f(x) = −		*( x + 1)*( x − 5)
	3

==========================

erw: skąd wiadomo że x₂=5 a nie x₁=5?

Janek191:: Jeżeli p = 2 , to x₂ > p i dlatego x₂ = 5

Janek191:: x₁ < p < x₂