7 zadań ze zbioru Kiełbasy - ciągi vdmath: Mam problem z 7 zadaniami:

	x		x		x
1. Wyznacz zbiór wartości funkcji f(x)=		+		+		+...., jeżeli
	x−2		(x−2)2		(x−2)3

	x		x		x
wyrażenie		+		+		+.... jest szeregiem geometrycznym.
	x−2		(x−2)2		(x−2)3

	1
Odp.: (−		;1) u (1; +∞)
	2

2. Rozwiąż równanie lim_(n→∞) (log₈ x + log_2/8 x + log_3/8 x +....+ log_n/8 x) =

	1+2+3+...+n
lim(n→∞)
	√n4 + 4

Odp.: x=2 3. Dla jakich wartości parametru a równanie a+asinx+asin²x+asin³x+....=sinx−0,5, gdzie lewa strona równania jest sumą nieskończonego ciągu geometrycznego, ma rozwiązania rzeczywiste?

	1
Odp.: −3<a≤
	16

4. Wyznacz te wartości parametru m, dla których równanie x−x³+x⁵−....=m+m²+m³+... ma rozwiązania, jeżeli wyrażenia po obu stronach równania są szeregami geometrycznymi zbieżnymi.

	1
Odp.: m∊(−1;		)
	3

5. Uczniowie pewnej szkoły zobowiązali się z okazji XX−lecia Polski Ludowej posadzić przy drodze 1200 drzewek w pewnym terminie. Po przepracowaniu jednego dnia postanowili skrócić czas pracy o 2 dni w ten sposób, że każdego dnia posadzą o 20 drzewek więcej niż poprzedniego. Obliczyć, w ciągu ilu dni uczniowie wykonali zobowiązanie i o ile procent skrócili czas pracy w stosunku do planowanego terminu. Odp.: 6 dni i o 25% 6. Wyznacz największą wartość parametru p, dla której granica ciągu (a_n) o wyrazie ogólnym

	(p3−2p+1)(4n6−2n+1)
an=		jest równa 1.
	(2n2−2n+1)3

	1+√5
Odp.: p=
	2

7. Drugi wyraz nieskończonego ciągu arytmetycznego (a_n) równy jest 1. Oblicz pierwszy wyraz

	a1+a2+a3+...+an		1
tego ciągu wiedząc, że limn→∞		=		.
	1−2n−3n2		3

Odp.: a₁=3 Te zadania ze mną wygrały na cały obszerny rozdział ciągów. Bardzo proszę o pomoc.

Janek191::

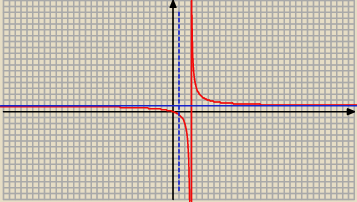
	x		x
f(x) =		+		+ ...
	x −2		( x − 2)2

	x
a1 =
	x − 2

	1		1
q =		oraz I		I < 1
	x − 2		x − 2

wtedy

	x		1		x
f (x) =		: [ 1 −		] =		; x ≠ 3
	x − 2		x − 2		x − 3

	1
oraz		< 1 ⇔ I x − 2 I > 1 ⇔( x < 1 lub x > 3 )
	I x − 2 I

	1		1
f( 1) =		= −
	1 − 3		2

Asymptota pozioma ma równanie f(x) = 1 więc

	1
ZWf = ( −		, 1 ) ∪ ( 1 ; + ∞ )
	2

===========================

vdmath: Janek191 dziękuję ma ktoś pomysł na pozostałe zadanka?

pigor: ...., nie lubię takie baterii zadań w jednym poście, bo nie chce mi się .... , ale wpadło mi w oko zad.6) −−−−−−−−−−−−−−−−−−−−−−− otóż, bardzo "mądra" treść zadania, a odpowiedź tkwi w rozwiązaniu ... niewinnego równania : ¹₈*4(p³−2p+1)=1 ⇔ p³−2p+1=2 ⇔ p³−2p−1=0 ⇔ ⇔ p^^3+p²−p²−p−p−1=0 ⇔ p²(p+1)−p(p+1)−1(p+1)=0 ⇔ ⇔ (p+1) (p²−p−1)=0 ⇔ (*) p= −1 v p²−p−1=0 i √Δ=√5, zatem p= ¹₂(1−√5) v p= ¹₂(1+√5), stąd i z (*) : p= −1< ¹₂(1−√5< ¹₂(1+√5 − szukana wartość p ...

vdmath: No tak, jak zawsze okazało się bardzo łatwe, tylko ciężko było wpaść na pomysł. Bardzo dziękuję pigor

paproć: Dlaczego w rozwiązniu Janek191 sprawdzana jest wartość f(1)? Dlaczego ta wartość ma znaczenie w wyznaczaniu zbioru wartości?

ICSP: zawsze sprawdza się wartości na krańcu dziedziny

werdi: skąd się wzięło f(x) =1