Podaj przykład funkcji Wlodek: Nieciągłej na przedziale [0,2], dla której f(0) * f(2)<0 i nie zachodzi teza twierdzenia Darboux (zapisz wzór funkcji lub narysuj jej wykres) Potrzebuję dobrze wytłumaczonego co i jak się dzieję

Wlodek: Pomocy

PW: To proste. Niech będzie nieciągła na przykład w punkcie x₀ = 1 i niech na przedziale [0,1] będzie stale dodatnia (cokolwiek rysujesz, np funkcję stałą f(x) = 3). Niech na przedziale (1, 2]] będzie stale ujemna.

Wlodek: Mógłbyś mi to narysować, bo nie bardzo rozumiem.

PW: Na przedziale domkniętym [0, 1] f(x) = 3. Na przedziale (lewostronnie otwartym, prawostronnie domkniętym) (1, 2] f(x) = −3. To taki najprostszy przykład, może być ich nieskończenie wiele. f(0) = 3, f(2) = −3, czyli f(0)·f(2) < 0 a funkcja nigdzie na przedziale [0,2] nie przyjmuje wartości 0. Przykład ten ilustruje ważność założenia "f jest ciągła" − bez tego założenia twierdzenie Darboux nie jest prawdziwe.

Wlodek: A czy funkcja x² jest funkcją nieciągłą na przedziale [0,2]?

PW: Zamorduję.

Prosiak: przedszkole otwierają o siódmej miałeś racje

Wlodek: Przepraszam, ale tego nie rozumiem

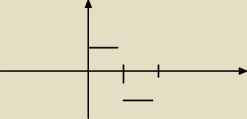
Wlodek: Jeżeli dobrze zrozumiałem wykres funkcji którą opisałeś powyżej

PW: Włodek, Prosiaczek śmieje się, bo wygląda na to, że nie chodziłeś na wykłady ani ćwiczenia − zadajesz pytania na poziomie przedszkola.

PW: Do wpisu z 18:03. Tak, tylko jeszcze "pełne kółko" na końcu górnego odcinka i "puste kółko" na początki dolnego.

Wlodek: Chciałem się tylko upewnić, jednak widać że nie ma głupich pytań tylko głupie odpowiedzi. W każdym razie dziękuję za naprowadzenie