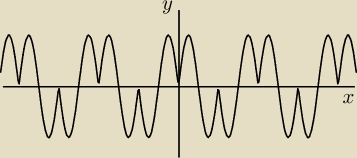
Wykres f(x)=2cosx*|sinx| dla x∊<0;2π>
KooT11: Witam serdecznie. Przychodzę z problemem, gdyż nie mam pojęcia jak się wziąć z to zadanie
(poziom matura rozszerzona).
Naszkicuj wykres funkcji f(x)=2cosx*|sinx| w zbiorze x∊<0;2π>
Wiem, że dla sinx>0 f(x)=2cosx*sinx
a dla sinx<0 f(x)=−2cosx*sinx
natomiast nie wiem jak to narysować na wykresie.
Wiem że 2cosx*sinx=(sinx+cosx)
2−1 ale nie wiem jak to zastosować i czy w ogóle to potrzebne

22 lut 14:50
wmboczek: 2sinxcosx=2sin2x
22 lut 14:53
wmboczek: 2sinxcosx=sin2x
22 lut 14:53
KooT11: aaa... W takim razie dzięki wielkie!
22 lut 15:23
AS:
|sin(x)| = sin(x) dla x ∊ <0,π>
|sin(x)|= −sin(x) dla x ∊ <π,2*π> w pierwszym okresie
Stąd odpowiednio
| | 1 | |
f(x) = cos(x)*sin(x) = |
| *sin(2*x) dla x ∊ <0,π> |
| | 2 | |
| | 1 | |
f(x) = −cos(x)*sin(x) = − |
| *sin(2*x) dla x ∊ <0,2*π> |
| | 2 | |
22 lut 15:30
AS: Poprawka − poknociłem,zgubiłem 2 w temacie
|sin(x)| = sin(x) dla x ∊ <0,π>
|sin(x)|= −sin(x) dla x ∊ <π,2*π> w pierwszym okresie
Stąd odpowiednio
f(x) = 2*cos(x)*sin(x) = = sin(2*x) dla x ∊ <0,π>
f(x) = −2*cos(x)*sin(x) = −sin(2*x) dla x ∊ <0,2*π>
22 lut 15:38

 |sin(x)| = sin(x) dla x ∊ <0,π>
|sin(x)|= −sin(x) dla x ∊ <π,2*π> w pierwszym okresie
Stąd odpowiednio
|sin(x)| = sin(x) dla x ∊ <0,π>
|sin(x)|= −sin(x) dla x ∊ <π,2*π> w pierwszym okresie
Stąd odpowiednio