KWADRATOWA
Zdzisiu: Wyznacz wartości parametru m, dla których suma odwrotności kwadratów dwóch różnych pierwiastków
równania x2+2mx−x−1=0 jest równa 3.
Δ>0
1/x12+1/x22=3
Δ=(2m−1)2+4=4m2−4m+5
I teraz Δ z m wychodzi ujemna?
22 lut 11:16
irena_1:
x
2+(2m−1)x−1=0
Δ=(2m−1)
2+4≥4
Dla dowolnej rzeczywistej liczby m równanie ma 2 różne pierwiastki rzeczywiste
x
1+x
2=−2m+1
x
1x
2=−1
| 1 | | 1 | | x12+x22 | |
| + |
| = |
| = |
| x12 | | x22 | | x12x22 | |
| | (x1+x2)2−2x1x2 | |
= |
| = |
| | (x1x2)2 | |
| | (−2m+1)2−2(−1) | | 4m2−4m+1+2 | |
= |
| = |
| = |
| | (−1)2 | | 1 | |
=4m
2−4m+3
4m
2−4m+3=3
4m
2−4m=0
4m(m−1)=0
m=0 lub m=1
22 lut 11:22
J:
skoro Δm jest ujemna, to oznacza,że Δ > 0 dla każdego m
22 lut 11:24
Jolanta: Δ=4m2−4m+1
po lewej stronie masz napisanie jak sie podnosi do kwadratu
22 lut 11:25
Jolanta: oczywiście +5

22 lut 11:28
Zdzisiu: dzięki wielkie

a moglibyście mi pomóc jeszcze rozwiązać to:
√x2+7 >
√2x + 3
√2
podnioslem to do kwadratu, x
2+7 zawsze jest dodatnie, więc nie muszę rozpisywać na moduły,
zatem:
x
2+7>2x
2+12x+18
−x
2−12x−11>0
Δ=144−44=100
x1=−1
x2=−11
x∊(−
∞;−11) ∪ (−1;
∞) a prawidłowy wynik z odpowiedzi to x∊(−
∞;−1)
Co jest źle?
22 lut 12:48
Zdzisiu: i jeszcze jedno: jak się rysuje takie funkcje:
a) f(x)=|x2+2x|−4
b)f(x)=|x2−4|+x2
22 lut 12:51
5-latek:
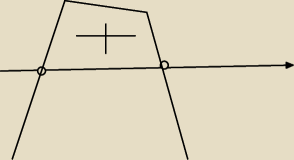
Po pierwsze x
2+7 nie zwiniesz do kwadratu z echcesz rozpisywac na moduly
Po drugie patrz rysunek
22 lut 12:55
J:
a) rysujesz f(x) = x2 +2x , odbijasz to co pod osią OX nad oś OX, przesuwasz o 4 w dół
b) dla x2 − 4 ≥ 0 rysujesz f(x) = 2x2 − 4
dla x2 − 4 < 0 rysujesz: f(x) = 4
22 lut 12:55
Zdzisiu: okej, rysowanie już rozumiem, ale tej nierówności, co 5−latek narysował wykres niestety dalej
nie

mógłby ktoś w całości napisać rozwiązanie
22 lut 12:57
5-latek: Tylko dlatego ze masz na imie jak moj brat to zapytam Cie czy dobrze przepisana jest tresc
zadania
czy prawa strona nierownosci ma byx taka > √2x+3√2 tzn czy ten x ma byc pod
pierwiastkiem vzy nie bo to jest duza roznica
22 lut 13:03
Zdzisiu: Dobrze przepisałem treść, tylko 2 jest pod pierwiastkiem, x nie
22 lut 13:05
Zdzisiu: i jeszcze jedna funkcja do narysowania, przepraszam, ze tak duzo: f(x)=|x2−9|−2x, nie mogę
zrobić tak jak podpunktu a, bo potem nie przesune o −2x? Muszę to całe rozpisaćna przypadki,
wyliczyć miejsca zerowe itd. czy jak?
22 lut 13:10
Zdzisiu: 
22 lut 13:47
Zdzisiu: pomoże ktoś?
22 lut 14:29
J:
dla x2− 9 ≥ 0 rysujesz: f(x) = x2 − 2x − 9
dla x2 − 9 <0 rysujesz: f(x) = −x2 − 2x + 9
22 lut 14:32
5-latek:
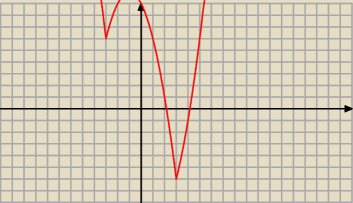
22 lut 14:36
Zdzisiu: dzięki, a to co 5−latek pytał czy dobrze przepisałem polecenie?
22 lut 14:52
Zdzisiu: 
22 lut 20:11
Zdzisiu: napisze jeszcze raz polecenie:
√x2+7 > √2x + 3√2
22 lut 20:22
Zdzisiu: pomożecie?

22 lut 20:39
5-latek: Mi wychodzi inny przedzial
Zapytaj Pania Mile a Pania Ete
22 lut 21:00
Zdzisiu: a tu jest jakieś PW czy coś? czy muszą po prostu wejść na ten temat?
22 lut 21:04
5-latek: Zaraz poproszse Mile
22 lut 21:07
Zdzisiu: ok, dzięki

22 lut 21:09
Zdzisiu: ogólnie mam problem z takimi zadaniami jak to lub
√x4−x2 ≤ 4−x
2, cały czas wychodzą mi złe
wyniki, podnoszę obie strony do kwadratu, w tych przypadkach prawą stronę wzorem skróconego
mnożenia, a i tak ciągle jest źle

22 lut 21:12
prosta: zbiór rozwiązań twojej nierówności to : x∊(−11,−1)
22 lut 21:12
Zdzisiu: tak mi wyszło, a w odp jest inaczej
22 lut 21:13
prosta: rozwiązanie x∊(−11,−1) obowiązuje w zakresie x≥−3 ( wtedy obie strony nierówności są nieujemne
i można podnieść obustronnie do kwadratu)
więc x∊<−3, −1)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
dla x<−3 lewa strona nierówności jest dodatnia a prawa strona ujemna, więc nierówność jest
prawdziwa dla x∊(−∞,−3)
22 lut 21:18
5-latek: To nie jest tak ze Ty sobie podnosisz do kwadratu
Zeby podniesc do potegi drugiej obie strony musisz miec zagwarantowane ze obie strony
nierownodsci sa nieujemne
22 lut 21:18
prosta: ogólna odpowiedź to suma tych dwóch przedziałów : x∊( −∞,−1)
22 lut 21:20
Zdzisiu: a jak się znajduje ten przedział, dla którego obie strony są nieujemne?
22 lut 21:24
Zdzisiu: i skąd wiadomo, że akurat wtedy w tym przedziale "dla x<−3 lewa strona nierówności jest
dodatnia a prawa strona ujemna, więc nierówność jest
prawdziwa dla x∊(−∞,−3)"
22 lut 21:29
prosta: √81>√2(x+3) lewa strona jest nieujemna
prawa będzie nieujemna, gdy x+3≥0
x≥−3
i przy takim założeniu obustronnie podnosimy do kwadratu
22 lut 21:30
Zdzisiu: a skąd wiadomo, że dla x<−3 nierówność jest prawdziwa dla x∊(−∞;3)? bo nie wyliczałeś tego
22 lut 21:32
prosta: po podniesieniu do kwadratu otrzymujemy : x∊(−11,−1)−−−−−−−> uwzględniamy wcześniejsze
założenie i mamy : x∊<−3,−1)
22 lut 21:32
Zdzisiu: czy to po prostu tak z założenia bierzemy?
22 lut 21:33
prosta: dla x<−3 nie trzeba wyliczać; po prawej stronie występuje liczba dodatnia( niezależnie od x) ,
po lewej ujemna ( bo x<3) . Stąd P>L.
22 lut 21:34
prosta: dodatnia>ujemna
22 lut 21:35
Mila:
Czy już wszystko jasne, czy dalej masz problem?
22 lut 21:38
Zdzisiu: rozumiem już, dzięki wielkie! mój bład polegał gównie na tym, że nie wiedziałem, że muszę
pierwsze ustalić x, dla których obie strony są nieujemne
22 lut 21:39
Zdzisiu: jednak nie do końca, bo dalej mam problem z tym przykłądem:
√x4−x2 ≤ 4−x2
22 lut 21:41
Zdzisiu: obie strony są dodanie dla −2≤x≤2, ale jak to wylicze to wychodzi x≤√16/7, a to nie zgadza
sie z wynikiem
22 lut 21:42
prosta: tutaj dziedzinę najpierw ustalamy, potem tak jak wyżej
22 lut 21:42
Zdzisiu: no to ustaliłem? czy coś źle?
22 lut 21:43
prosta: D: x4−x2≥0
x2(x2−1)≥0
x∊(−∞,−1>∪<1,∞)
po uwzględnieniu założenia: x∊<−2,−1>∪<1,2>
22 lut 21:48
prosta: a po podniesieniu obustronnym mamy x∊<−√16/7,√16/7>
22 lut 21:50
prosta: pewnie będzie x∊<−√16/7,−1>∪<−1,√16/7>
22 lut 21:51
Zdzisiu: no ok, wyliczyłem, że x ≤ 4√7/7, i ak znaleźć koncowe rozwiązanie?
22 lut 21:53
Zdzisiu: to co napisałeś to rozumiem, ale w odp jest jeszcze 0, które nie mam pojęcia skąd sie bierze
22 lut 21:53
prosta: ....fakt. 0 też należy do dziedziny ....i warto sprawdzić co się dzieje dla zera
L=0, P=4
22 lut 21:56
prosta: czyli 0 należy do zbioru rozwiązań
22 lut 21:56
Zdzisiu: ale dlaczego należy, jeżeli lewa strona nie jest równa prawej?
22 lut 21:58
prosta: po zestawieniu prawidłowej dziedziny D; x∊(−∞,−1>∪<1,∞)∪{0}
i nierówności x∊<−√16/7,√16/7>
mamy odpowiedź
22 lut 21:59
prosta: lewa strona jest mniejsza od prawej

22 lut 22:00
Zdzisiu: czyli 0 należy do dziedziny, ponieważ z pozostałej części dziedziny wynika, że lewa strona jest
mniejsza od prawej? takie trochę dziwne, albo nadal czegoś nie rozumiem
22 lut 22:02
Mila:
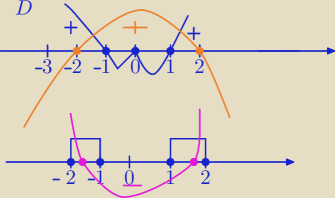
D:
x
4−x
2≥0⇔
x
2(x
2−1)≥0⇔
x
2*(x−1)*(x+1)≥0⇔x≤−1 lub x≥1
Ponieważ
√.. z definicji jest ≥0 tp prawa strona też musi być dodatnia lub równa 0 , aby
nierówność miała sens.
4−x
2≥0⇔(2−x)*(2+x)≥0 prabola skierowana w dół.⇔
x∊<−2,2>
Nierówność rozważamy w przedziałach:
<−2,1>∪<1,2>
√x4−x2≤4−x
2 /
2
x
4−x
2≤16−8x
2+x
4⇔
7x
2−16≤0 /:7
| | 4 | | 4 | |
(x− |
| ) *(x+ |
| )≤0 parabola skierowana do góry |
| | √7 | | √7 | |
Odpowiedź:
=====================
22 lut 22:04
Zdzisiu: Mila też nie uwzględniła tego zera?
22 lut 22:06
Zdzisiu: więc wytłumaczy mi ktoś jak z tym zerem?

22 lut 22:14
prosta: na to wygląda....w dziedzinie też brakuje zera
22 lut 22:15
prosta: przecież wcześniej już było:
po zestawieniu prawidłowej dziedziny D; x∊(−∞,−1>∪<1,∞)∪{0} i nierówności x∊<−√16/7,√16/7> mamy
odpowiedź
22 lut 22:16
prosta: Mila też nie zauważyła, że 0 należy do dziedziny
22 lut 22:18
Mila:
No tak , masz rację, chyba dlatego, że późno.
Trzeba jeszcze dołączyć 0.
D nierówności: x∊<−2,−1>∪{0}∪<1,2>
odp :
| | 4 | | 4 | |
x∊<− |
| ,−1>∪{0}∪<1,− |
| > |
| | √7 | | √7 | |
Teraz jasne?
22 lut 22:21
Mila:
Przecież, to powinieneś zobaczyć na osi, które narysowałam.
22 lut 22:22
Zdzisiu: no widzę to na osi, ale nadal nie rozumiem skąd ono sie bierze, ja bym go na osi nie uwzględnił

22 lut 22:33
Zdzisiu: nie rozumiem skąd 0 w dziedzinie, chyba, że po prostu zero zawsze trzeba sprawdzić osobno?
22 lut 22:34
prosta: do dziedziny należą liczby z przedziałów (−∞,−1) oraz (1,∞) oraz te, dla których wartość pod
pierwiastkiem jest równa zero: są to liczby : −1,1,0.
Zatem przedziały domykają się a zero należy podać w jednoelementowym zbiorze
22 lut 22:38
prosta: widać to na rysunku Mili....zapełnione kropki dla −1,0,1
22 lut 22:39
Mila:
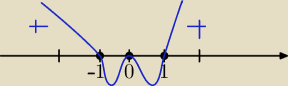
Wyrażenie pod pierwiastkiem nieujemne⇔
x
2*( x−1)*(x+1)≥0 i teraz oś, na której zaznaczam 3 miejsca zerowe.
x=0, x=1, x=−1
0 jest pierwiastkiem podwójnym o parzystej krotności, zatem masz odbicie na osi.
x∊(−
∞,−1>∪{0} ∪ <1,
∞)
22 lut 22:41
Zdzisiu: Rozumiem

dzięki wielkie
22 lut 22:43
Zdzisiu: a moglibyście jeszcze sprawdzić to zadanko?
Dla jakich wartości parametru m część wspólna przedziałów: A=(−∞;m3−m> i B=<2m−2;∞) jest
zbiorem pustym?
m3−m<2m−2
m3−3m+2<0
Dla m=1 wielomian się zeruje.
Podzieliłem schematem Hornera przez m−1,
wyszło m2−m−2<0, Δ=9 m1=−1 m2=2
zatem
m∊(−∞;−1)∪(1;2)
W odp jest (−∞;−2)
22 lut 23:30
Zdzisiu: znalazłem, że również dla m=−2 się zeruje, ale przecież nie będę sprawdzał wszystkich liczb,
które dany wielomian zerują, skąd to jeszcze wynika, że −2?
22 lut 23:40
Zdzisiu: 
23 lut 15:28
Mila:
Błędnie rozwiązałeś nierówność.
Konretnie, dzielenie przez (m−1) popraw.
23 lut 16:26
Zdzisiu: Schemat Hornera:
(m3−3m+2):(m−1)
1 0 −3 2
1 1 −2 0
m2−m−2<0
co jest źle?
23 lut 16:31
Mila:
Gdzie tam widzisz (− ) przy drugiej jedynce?
23 lut 16:34
Zdzisiu: no racja, ale teraz mam przedział (−2;1)
23 lut 16:37
Mila:
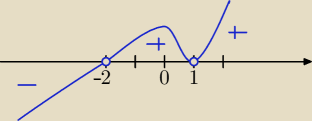
Teraz masz:
(m−1)
2*(m+2)<0 patrz na oś
m=1 jest pierwiastkiem podwójnym ( parzystej kroktności)
m<−2
23 lut 16:51
Zdzisiu: (m−1)2*(m+2)≠m2+m−2 przecież
23 lut 21:03
Zdzisiu: (m−1)2*(m+2)≠m2+m−2
23 lut 21:04
Zdzisiu: (m−1)(m+2)=m2+m−2, wtedy nie jest pierwiastkiem parzystej krotności
23 lut 21:05
Mila:
To jest Twoja wyjściowa nierówność:
m3−m<2m−2
I rozwiązanie podałam dla tej nierówności.
Może wypisuj sobie w punktach czynności, bo w połowie zadania zapominasz o co chodzi.
23 lut 21:08
Zdzisiu: skupiłem się na tej po przekształceniu, masz racje, wszystko sie zgadza, dzieki wielkie

23 lut 21:37
Mila:
23 lut 21:43

 a moglibyście mi pomóc jeszcze rozwiązać to:
√x2+7 > √2x + 3√2
podnioslem to do kwadratu, x2+7 zawsze jest dodatnie, więc nie muszę rozpisywać na moduły,
zatem:
x2+7>2x2+12x+18
−x2−12x−11>0
Δ=144−44=100
x1=−1
x2=−11
x∊(−∞;−11) ∪ (−1;∞) a prawidłowy wynik z odpowiedzi to x∊(−∞;−1)
Co jest źle?
a moglibyście mi pomóc jeszcze rozwiązać to:
√x2+7 > √2x + 3√2
podnioslem to do kwadratu, x2+7 zawsze jest dodatnie, więc nie muszę rozpisywać na moduły,
zatem:
x2+7>2x2+12x+18
−x2−12x−11>0
Δ=144−44=100
x1=−1
x2=−11
x∊(−∞;−11) ∪ (−1;∞) a prawidłowy wynik z odpowiedzi to x∊(−∞;−1)
Co jest źle?
 Po pierwsze x2+7 nie zwiniesz do kwadratu z echcesz rozpisywac na moduly
Po drugie patrz rysunek
Po pierwsze x2+7 nie zwiniesz do kwadratu z echcesz rozpisywac na moduly
Po drugie patrz rysunek
 mógłby ktoś w całości napisać rozwiązanie
mógłby ktoś w całości napisać rozwiązanie







 D:
x4−x2≥0⇔
x2(x2−1)≥0⇔
x2*(x−1)*(x+1)≥0⇔x≤−1 lub x≥1
Ponieważ √.. z definicji jest ≥0 tp prawa strona też musi być dodatnia lub równa 0 , aby
nierówność miała sens.
4−x2≥0⇔(2−x)*(2+x)≥0 prabola skierowana w dół.⇔
x∊<−2,2>
Nierówność rozważamy w przedziałach:
<−2,1>∪<1,2>
√x4−x2≤4−x2 /2
x4−x2≤16−8x2+x4⇔
7x2−16≤0 /:7
D:
x4−x2≥0⇔
x2(x2−1)≥0⇔
x2*(x−1)*(x+1)≥0⇔x≤−1 lub x≥1
Ponieważ √.. z definicji jest ≥0 tp prawa strona też musi być dodatnia lub równa 0 , aby
nierówność miała sens.
4−x2≥0⇔(2−x)*(2+x)≥0 prabola skierowana w dół.⇔
x∊<−2,2>
Nierówność rozważamy w przedziałach:
<−2,1>∪<1,2>
√x4−x2≤4−x2 /2
x4−x2≤16−8x2+x4⇔
7x2−16≤0 /:7


 Wyrażenie pod pierwiastkiem nieujemne⇔
x2*( x−1)*(x+1)≥0 i teraz oś, na której zaznaczam 3 miejsca zerowe.
x=0, x=1, x=−1
0 jest pierwiastkiem podwójnym o parzystej krotności, zatem masz odbicie na osi.
x∊(−∞,−1>∪{0} ∪ <1,∞)
Wyrażenie pod pierwiastkiem nieujemne⇔
x2*( x−1)*(x+1)≥0 i teraz oś, na której zaznaczam 3 miejsca zerowe.
x=0, x=1, x=−1
0 jest pierwiastkiem podwójnym o parzystej krotności, zatem masz odbicie na osi.
x∊(−∞,−1>∪{0} ∪ <1,∞)
 dzięki wielkie
dzięki wielkie

 Teraz masz:
(m−1)2*(m+2)<0 patrz na oś
m=1 jest pierwiastkiem podwójnym ( parzystej kroktności)
m<−2
Teraz masz:
(m−1)2*(m+2)<0 patrz na oś
m=1 jest pierwiastkiem podwójnym ( parzystej kroktności)
m<−2
