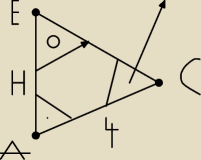
 W graniastosłupie prawidłowym czworokątnym ABCDEFGH przekątna AC podstawy ma długość 4. Kąt ACE
jest równy 60°. Oblicz objętość ostrosłupa ABCDE przedstawionego na poniższym rysunku.
https://www.google.pl/search?q=w+graniastos%C5%82upie+prawid%C5%82owym+czworok%C4%85tnym+abcdefgh+przek%C4%85tna+ac+podstawy+ma+d%C5%82ugo%C5%9B%C4%87+4&biw=1366&bih=637&source=lnms&tbm=isch&sa=X&ei=mtroVK2SAYLzatmogoAH&ved=0CAcQ_AUoAg#imgdii=_&imgrc=CuPFzRNM0ewMjM%253A%3BX3g8LdD55iBUjM%3Bhttp%253A%252F%252F2.bp.blogspot.com%252F-Yj0ToArCqdA%252FUV7XxEfo_8I%252FAAAAAAAAADo%252FSXMXJQBAc5g%252Fs1600%252Fstopnie.png%3Bhttp%253A%252F%252Fmatematyka-tak.blogspot.com%252F2013%252F04%252Fmatura-2012-poziom-podstawowy-zadania.html%3B213%3B221
Legenda
strzałka − kąt 60°.
kąt oznaczony kołem − kąt 30°.
kąt oznaczony kropką − kąt prosty.
Vo − objętość ostrosłupa.
I chciałbym, aby było sprawdzone
d=a√2
d=2√2
PP=(2√2)2=8{j}2
Z rysunku tg 30°=4/H
√3/3=4/h−−−−
H=4√3
Vo=8*4√3/3
V=32√3/3{j}3
W graniastosłupie prawidłowym czworokątnym ABCDEFGH przekątna AC podstawy ma długość 4. Kąt ACE
jest równy 60°. Oblicz objętość ostrosłupa ABCDE przedstawionego na poniższym rysunku.
https://www.google.pl/search?q=w+graniastos%C5%82upie+prawid%C5%82owym+czworok%C4%85tnym+abcdefgh+przek%C4%85tna+ac+podstawy+ma+d%C5%82ugo%C5%9B%C4%87+4&biw=1366&bih=637&source=lnms&tbm=isch&sa=X&ei=mtroVK2SAYLzatmogoAH&ved=0CAcQ_AUoAg#imgdii=_&imgrc=CuPFzRNM0ewMjM%253A%3BX3g8LdD55iBUjM%3Bhttp%253A%252F%252F2.bp.blogspot.com%252F-Yj0ToArCqdA%252FUV7XxEfo_8I%252FAAAAAAAAADo%252FSXMXJQBAc5g%252Fs1600%252Fstopnie.png%3Bhttp%253A%252F%252Fmatematyka-tak.blogspot.com%252F2013%252F04%252Fmatura-2012-poziom-podstawowy-zadania.html%3B213%3B221
Legenda
strzałka − kąt 60°.
kąt oznaczony kołem − kąt 30°.
kąt oznaczony kropką − kąt prosty.
Vo − objętość ostrosłupa.
I chciałbym, aby było sprawdzone
d=a√2
d=2√2
PP=(2√2)2=8{j}2
Z rysunku tg 30°=4/H
√3/3=4/h−−−−
H=4√3
Vo=8*4√3/3
V=32√3/3{j}3
