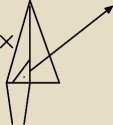https://www.google.pl/search?q=dany+jest+graniastos%C5%82up+prawid%C5%82owy+tr%C3%B3jkatny+abcdef+o+podstawach&biw=1366&bih=637&source=lnms&tbm=isch&sa=X&ei=VbroVNiVFdTfarDWgjA&ved=0CAYQ_AUoAQ#imgdii=_&imgrc=6ifLohCC-VXJUM%253A%3BQptot5KHAUe47M%3Bhttp%253A%252F%252F2.bp.blogspot.com%252F-5MHnkIzzZXY%252FUKifJAqJ3jI%252FAAAAAAAAAWE%252FI8sWmyYAg_0%252Fs1600%252Fzadpp34.jpg%3Bhttp%253A%252F%252Ftwojamatma.blogspot.com%252F2012%252F12%252Fmatura-podstawowa-czerwiec-2012-zadanie_12.html%3B410%3B420
Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach
bocznych AD, BE i CF (zobacz rysunek). Długość krawędzi podstawy AB jest równa 8, a pole
trójkąta ABF jest równe 52. Oblicz objętość tego graniastosłupa.
I chciałbym o sprawdzenie:
strzałka=13
dwie proste=4.
W podstawie jest trójkąt równoboczny więc wszystkie boki mają po 8.
Pole trójkąt ABF jest równe 52.
52=8*H2−−−−−−−h=13.
42+132=x2
16+169=x2
185=x2
x=√185
CA=8
FA=√185
CA2+FC2=FA2
82+X2=√1852
64+X2=185
X2=121
X=11
Pole podstawy= a2√3/4
h=a√3/2
h=8√3/4=64√3/4=16√3
V=16√3*11=176√3{j}3
.
