okrąg ola: Promien okregu wpisanego w trójkat o wierzchołkach w punktach (9, 2), (0, 20), (−15,−10) jest równy a)5√3 b) 540 c) 3√5 d)15√5

irena_1: Trójkąt jest prostokątny a²=(9−0)²+(2−20)²=81+324=405 b²=(−15−9)²+(−10−2)²=576+144=720 c²=(−15−0)²+(−10−20)²=225+900=1125 a²+b²=c² a=9√5 b=12√5 c=15√5 a+b=c+2r 21√5=15√5+2r 2r=6√5 r=3√5

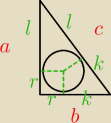
irena_1: a=r+l b=r+k c=l+k a+b=r+l+r+k=(l+k)+2r=c+2r