zadanko Blue: Równanie |m−x|+|x−5|=9 ma nieskończenie wiele rozwiązań dla A. m= −14 B. m= 4 C. m=5 D. m= 14 Mógłby ktoś to wytłumaczyć?

Blue: dla m = 14 jest nieskończenie wiele rozwiązań w przedziale <5,14), ale dla m=4 też jest nieskończenie wiele w przedziale (−∞,4>....

Kacper: blue rozwiąż równanie |4−x|+|x−5|=9

pigor: ..., najlepiej to widać na osi Ox z określenia na niej odległości i tak : |m−x|+|x−5|=9 ⇔ |x−m|+|x−5|=9 , to suma odległości x−ów od −5 i m jest równa 9 ⇔ m=14, czyli dla ∞ wielu x∊<−5;14> pozostałe wartości m nie spełniają warunek istnienia ∞ wielu rozwiązań; −−−−−−−−−−−−−−−−−−−−−−−− np. gdy m=4 suma |x−4|+|x−5|= 9 ⇔ x∊{0,9} (tylko dwa elementy x=0, x=9 spełniają to równanie), analogicznie m<4 ....

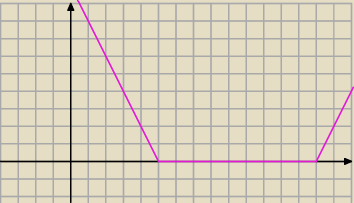
Tadeusz: chyba raczej |14−x|+|x−5|=9

pigor: ,,,;, dzięki no jasne,przepraszam, ... transmisja moich danych mózg − ekran zawiodła, miało być x∊<5;14> .

Tadeusz: ... przecież tu nikt nie pyta o x .... − DLA JAKIEGO m

pigor: ..; kurde, oczywiście m∊<5;14> ; to skutki jak skusiłem się wytłumaczyć rzeczy ... i przedobrzyłem . przepraszam, może ktoś kompetentny to wywalić,

Tadeusz: ... oj pigorku − ... tylko dla m=14

pigor: ..., no nie; wywalcie to i już, proszę; po co mi to a ja tylko chciałem niepotrzebnie − jak widać − pokazać, że tylko m=14 daje te nieskończenie wiele x∊< 5;14> i wcale nie miałem na myśli płaszczyzny z XOY i tyle, kropka.

Tadeusz: ... nie przeżywaj tak −

Eta:

jkl: kolejny temat idiotów hahahha

Tadeusz: masz rację jkl ... jesteś idiotą ... tylko idioci "sami hahaja się" z tego co mówią

Blue: Dziękuję Wam , chyba popełniłam jakieś błędy w obliczeniach..