KWADRAT ola: W kwadracie ABCD, o bokach długosci 2, punkt K jest srodkiem boku CD. Przez punkty A,B i K poprowadzono okrag. Wówczas promien tego okregu równy jest?

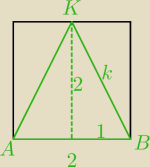
irena_1: k=√5 R− szukany promień okręgu opisanego na trójkącie ABK Z pola trójkąta:

2*2		2√5*√5
	=
2		4R

8R=10

	5
R=
	4

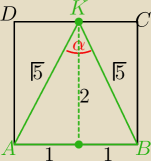Eta: 2 sposób

	5		4
P(ABK)=2 i P(ABK)=		*sinα ⇒ sinα=
	2		5

Z tw. sinusów

	2		4
2R=		⇒ R=
	sinα		5

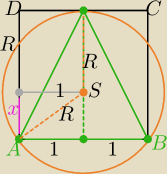Eta: 3 sposób x= 2−R

	5
Z tw. Pitagorasa R2=1+(2−R)2 ⇒ 4R=5 ⇒ R=
	4

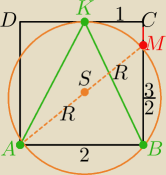Eta: 4 sposób Z twierdzenia o siecznej i stycznej |KC|²= |CB|*|CM| i |BM|=2−|CM|

	1		3
1=2*|CM| ⇒ |CM|=		to |BM|=
	2		2

|AM|=2R, R>0 i z tw. Pitagorasa w trójkącie ABM

	9		25		25		5
(2R)2= 4+		⇒4R2=		⇒ R2=		⇒ R=
	4		4		16		4

I mamy wyciągnięte prawie wszystkie "armaty" ( bo może ktoś jeszcze dorzuci inne sposoby