Czesc Misiek: Jak to ruszyć? "Dany jest ostrosłup prawidłowy sześciokątny. Krawędź boczna ostrosłupa jest dwa razy dłuższa od krawędzi jego podstawy. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa."

irena_1:

	a
h2+(		)2=(2a)2
	2

	1		15
h2=4a2−		a2=		a2
	4		4

	√15
h=		a
	2

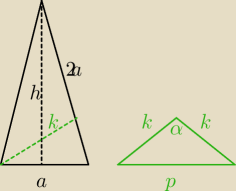
p − krótsza przekątna sześciokąta o boku a p=a√3 Z twierdzenia cosinusów p²=2k²−2k² cosα

	15
(a√3)2=2*		a2(1−cosα)
	4

	15
3a2=		a2(1−cosα)
	2

	2
1−cosα=3*
	15

	2
1−cosα=
	5

	3
cosα=
	5