Stereometria Marta: Bardzo proszę o pomoc: 1 Długość trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka tworzą ciąg geometryczny o sumie 19. Objętość prostopadłościanu jest równa 216. Wyznacz pole powierzchni całkowitej tego prostopadłościanu. 2. Przekątna przekroju osiowego walca jest nachylona do podstawy walca pod kątem α takim, że tg α= ²₃ 3. Objetość kuli jest równa 36π. Oblicz powierzchnie tej kuli. Obliczyłam i wyszło mi r=3, a pole=36π dobrze

Mateusz: 1) Oznaczamy a ,b ,c krawędzie prostopadłościanu

	x
a =		b = x c = xq =>
	q

abc = x³ = 216 x = 6

	1
S = a + b + c = x(		+ 1 +q) = 16 gdzie q≠0 i otrzymujemy
	q

	19
1+ q +q2 =		*q
	6

6+6q+6q² = 19q 6−13q +q² = 0 => dalej juz poradzisz sobie z dokonczeniem

Bogdan: Zadanie 1 można też rozwiązać tak: Ciąg: a, b, c jest geometryczny, a, b, c ∊ R₊ b² = ac (z własności ciągu geometrycznego), V = abc = 216 ⇒ b²*b = 216 ⇒ b³ = 216 ⇒ b = 6 ⇒ ac = 36 a + b + c = 19 ⇒ a + c = 19 − b ⇒ a + c = 13 Pole P = 2ab + 2ac + 2bc = 2b(a + c) + 2ac = 2*6*13 + 2*36 = ...

Marta: czyli Pole =228

Bogdan: tak, P = 228

Marta: a jak mam zrobić 2 i 3

Marta: tzn. 2 bo 3 zrobiłam tylko nie wiem czy dobrze

Mateusz: A co masz w 2 do policzenia 3 skorzystaj ze wzoru na objętość kuli i policz jej promień a potem policz powierzchnię te wzory znajdziesz tu https://matematykaszkolna.pl/strona/1005.html

Bogdan: W zadaniu 3 masz dobre wyniki. Jakie jest polecenie w zadaniu 2 ?

Marta: 2. Przekątna przekroju osiowego walca jest nachylona do podstawy walca pod kątem α takim, że tg α= ²₃ . Promień podstawy walca ma długość 24, wyznacz pole powierzchni bocznej tego walca.

Marta: jak podejść do tego 2 zadania

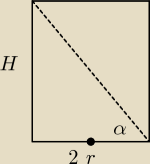
Nikka: P_pb = H*2πr (pole powierzchni bocznej to prostokąt o bokach długości równych H i 2πr) H − wysokość walca r − promień podstawy

	2
tgα =
	3

r = 24

	H
tgα =
	2r

2		H
	=		→ H = 32
3		48

P_pb = 32*2π*24 = 1536π

Marta: dziękuję bardzo za pomoc