Pomożecie to mi narysować i obliczyć będę bardzo wdzięczna bogusia: 4−2x a) Naszkicuj wykres funkcji f(x) = −−−−−− , x∊R − {0} i na jego podstawie opisz własności funkcji x b) Oblicz, dla jakich argumentów funkcja f osiąga wartości mniejsze niż funkcja 8 g(x) = −−−−−− . x+3

Nikka: b) do rozwiązania jest nierówność f(x) < g(x)

4−2x		8
	<
x		x+3

D: x≠0 i x+3≠0 D: x≠0 i x≠ −3

4−2x		8
	−		< 0
x		x+3

(4−2x)(x+3) − 8x
	< 0
x(x+3)

−2x2 − 10x + 12
	< 0 |:(−2)
x(x+3)

x2 + 5x − 6
	> 0
x(x+3)

(x² + 5x − 6)*x*(x+3) > 0 Δ = 25+24 = 49 √Δ = 7 x = −6 lub x = 1 x(x−1)(x+6)(x+3) > 0 i x∊D x∊(−∞,−6)∪(−3,0)∪(1,∞)

bogusia: nie mam szczęścia do pomocy chyba

Nikka:

	4
f(x) =		− 2
	x

	4
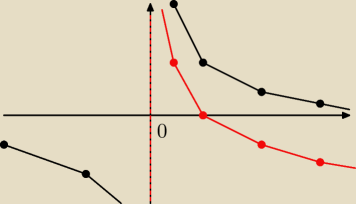
Rysujesz wykres funkcji h(x) =		i przesuwasz o dwie jednostki w dół − w ten sposób
	x

otrzymasz wykres funkcji f(x). Przesunąć trzeba obie części wykresu − mnie się tutaj nie zmieściło (jedna część kolorem czerwonym).

bogusia: przepraszam ze pytam ale jakie liczy były podstawione za x

Nikka: weź sobie np. 1,2, 4, 8 i −1, −2, −4 (tak, żeby było łatwo podzielić) Funkcja f(x) ma dwie asymptoty pionową o równaniu x=0 i poziomą o równaniu y= −2. Jak będziesz rysować wykres, wykres nie może tych prostych przecinać .

bogusia: ♥

Nikka: Własności: 1. D_f = R \ {0} 2. Zw = R \ {−2} 3. Asymptoty: x=0 − pionowa, y = −2 pozioma 4. Miejsce zerowe x_o = 2 (4−2x = 0 → x = 2) 5. Funkcja malejąca w całej dziedzinie.

Nikka: 6. Nie jest parzysta.