Stereometria Marta: Bardzo proszę o pomoc: 1. Objętość stożka równa jest 100π, a tworząca tworzy z podstawa kąt 30^o. Oblicz pole powierzchni bocznej tego stożka. 2. W ostrosłupie prawidłowym trójkątnym krawędzie boczne są dwa razy dłuższe od krawędzi podstawy. a) wyznacz sinus kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy b) Wyznacz długość krawędzi podstawy tak, aby objętość ostrosłupa wynosiła ²₃ √11

Marta: a tu czy ktoś pomoże

Alinka: Zadanie 1. O=πr²+πrl, gdzie r − to promień, l − tworząca πr²+πrl=100π r²+rl=100 tworząca tworzy z podstawą kąt 30^o, zatem korzystając z funkcji trygonometrycznych cos30⁰=^r_l Ułóż układ równań wyznacz r i l, a następnie podstawa do wzoru na pole pow bocznej P_b=πrl

Nikka: To co napisałaś Alinko to nie jest wzór na objętość stożka !

Nikka:

	1
V =		πr2 * H
	3

Alinka: sorki racja wstyd mi

Alinka: tak to jest gdy robi się dwie rzeczy na raz

Marta: ale ja nie wiem co i jak mam obliczyć z tej objętości jak zrobić te zadania

Bogdan:

	1		1
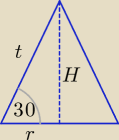
Proszę zauważyć, że objętość stożka V =		πr2*H ⇒		πr2*H = 100π
	3		3

Alinka: Poprawiam się zatem ¹₃ πr²*H=100π ¹₃r²*H=100 tg30^o=^H_r

Marta: czyli √3/3=H/r i jak ma to dalej rozwiązć 3H=√3 r

Marta: co mam dalej zrobić

Bogdan:

	√3		H
Z zależności		=		wyznacz H i wstaw do równania r2H = 300, stąd
	3		r

wyznacz r, potem długość tworzącej t z odpowiedniej funkcji trygonometrycznej kąta 30^o.

Marta: czyli H= √3/3 r tak

Nikka: tak

Marta: sin α= ^t_H sin 30^o=√3/3 r ¹₂=√3/3 r i co dalej

Nikka:

	H
tgα =
	r

√3		H		√3
	=		→ H =		*r
3		r		3

Podstawiam H do wzoru na objętość i obliczam r :

	1		√3
100π =		π r2*		*r
	3		3

	1		√3
100π =		π *		*r[3}
	3		3

	900
r3 =		→ r= 10√3
	√3

Obliczamy l (na rysunku t − tworząca) :

	r
cos30o =
	l

√3		10√3
	=		→ l= 20
2		l

P_pb = πrl = π*10√3*20 = 200√3π

Marta: a czy ktoś pomoże mi zrobić 2 zadanie

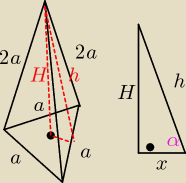
Nikka: Ostrosłup prawidłowy trójkątny ma w podstawie trójkąt równoboczny. Długość jego boku oznaczmy przez a (krawędź podstawy). Krawędź boczna ostrosłupa ma wtedy długość 2a.

	1
V=		Pp*H
	3

	√3
Pp =		a2
	4

h − wysokość ściany bocznej h obliczamy z tw. Pitagorasa (dla ściany bocznej, która jest trójkątem równoramiennym o podstawie a i ramionach równych 2a) :

	a		√15
h2 = (2a)2 − (		)2 → h =		a
	2		2

Następnie obliczamy wysokość ostrosłupa z trójkąta z rysunku (z tw. Pitagorasa): h² = H²+x²

	1		1		√3		√3
odcinek x to		wysokości podstawy czyli x =		*		a =		a
	3		3		2		6

	√15		√3
H2 = (		a)2 − (		a)2
	2		6

	44		√11
H2 =		a2 → H =		a
	12		√3

czyli

2		1		√3		√11
	√11 =		*		a2*		a → a3 = 8 → a=2
3		3		4		√3

Nikka: a)

	H
sinα =
	h

	√11		√15
sinα = (		*a) : (		a)
	√3		2

	√65
sinα =
	15

mam nadzieję, że nigdzie nie namieszałam (dawno nie robiłam zadań ze stereometrii)... i że jest ok

Marta: wielkie dzięki czyli a=2 to jest długość krawędzi czyli odpowiedź na podpunkt b tak

Nikka: na to wychodzi

Marta: jeszcze raz bardzo dziękuję

Nikka: nie ma za co (oby było dobrze)

Bogdan:

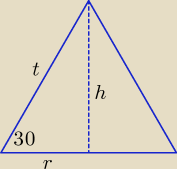
	1		3000
1.		πr2h = 1000π ⇒ h =
	3		r2

h		h		√3		3000
	= tg30o ⇒		=		⇒ r = √3h = √3 *		⇒
r		r		3		r2

r³ = 3000√3 = √3² * 10³ * √3 = √3³ * 10³ ⇒ r = 10√3

r		r		√3		2r		2
	= cos30o ⇒		=		⇒ t =		=		* 10√3 = 20
t		t		2		√3		√3

Pole P_B = πrt = π * 10√3 * 20 = 200√3π

Marta: bardzo dziękuje a czy te 2 zadanie jest dobrze

Bogdan:

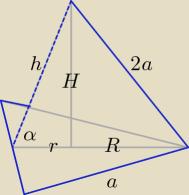
	1		3		1		3
R =		a√3, R2 =		a2, r =		a√3, r2 =		a2
	3		9		6		36

	1
H = √4a2 − R2 =		a√33
	3

	1
h = √H2 + r2 =		a√15
	2

	H
sinα =		= ... dokończ
	h

	1		1		1		2
Objętość		*		a2√3 *		a√33 =		√11 ⇒ a = 2
	3		4		3		3

Marta: sinα=√15*6√33?

Marta: a wracając do zadania 1 to: ^h_r=^√3₃⇒r=√3h skąd to jak ja licze to wychodzi mi r=h√3

Bogdan: Przecież podałem: r = √3h, a nie r = √3h

Bogdan: Podaj sinα jeszcze raz w zadaniu 2.

Marta: aha przepraszam, nie zauważyłam, a ten sin to penie źle policzyłam co

Marta: sin α=¹₂*2√15/²₃√33=√15*³₂√33 i nie wiem jak dalej

Bogdan:

	H		1   a√33   3		6
sinα =		=		*		=
	h		1   a√15   2		6

	2 * √3 * √11		√5		2√55
=		*		=
	3 * √3 * √5		√5		15

Marta: Bardzo dziękuje za pomoc

Nikka: a ja się pomyliłam w obliczeniach

	2√55
faktycznie sinα =		( źle pomnożyłam ułamki)
	15