Pole obszaru Petrus: Czy mógłby mi ktoś pomóc z tym zadaniem. W ogóle nie wiem jak się za to zabrać Obliczyć pole obszaru zawartego między wykresami funkcji f(x)=x²+1 i g(x)=2x+1

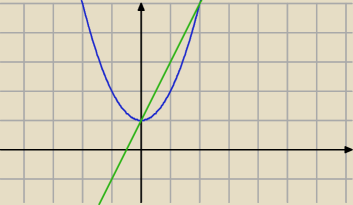
Qulka: całka (górna − dolna) w zakresie od 0 do 2 ∫2x+1−x²−1 dx = ∫2x−x² dx

Mila: 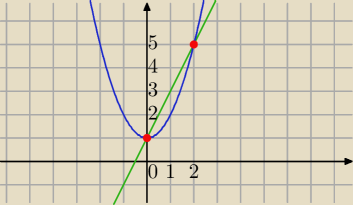f(x)=x²+1 g(x)=2x+1 x²+1=2x+1 x²−2x=0 x(x−2)=0 x=0 lub x=2

	1		1
P=0∫2(2x+1−x2−1)dx=0∫2(2x−x2) dx=[		*2x2−		x3]02=
	2		3

dalej poradzisz sobie?

Petrus: Czyli najpierw wyznaczam miejsca zerowe i rysuje wykres. Ok. "Całka(górna − dolna)" − masz na myśli całkę oznaczoną? I dlaczego akurat od 0 do 2?

Qulka: mam na myśli funkcje... od wzoru tej co jest wyżej odejmujesz tą co jest niżej

Qulka: bo w x= 0 i w 2 się przecinają funkcje

Petrus: Dzięki za pomoc, po prostu nie wiedziałem od jakiej strony się za to zabrać bo nie miałem materiałów z tego

	1		1		1		1		8
=(		* 2 * 22 −		* 23) − (		* 2 * 02 −		* 03) = −
	2		3		2		3		3

Prawidłowo?

Mila: Nie . cd. 20:54

	1
[x2−		x3]02=
	3

	1		2
=22−		*8=4−2−		=...
	3		3

Qulka: 4− 8/3 =4/3 =

Petrus: Okej, głupi błąd Ale już rozumiem, dziękuję za pomoc!

Mila: