1 Adam: całka podwójna: ∫∫xe^ydxdy ogr. krzywymi y=0 y=x, y=2−x jaka krzywa ogranicza z góry, a która z dołu ?

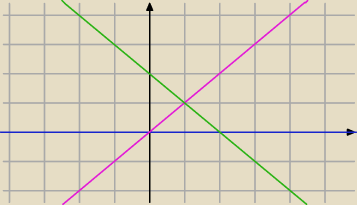
Gray: y=x ← różowe y=2−x ← zielone y=0 ← niebieskie Wnioski nasuwają się same.

Gray: Zamień na całkę iterowaną: ∫_[0,1] ∫_[y,2−y]xe^y dxdy

Adam: ok, tylko nie będzie tutaj obszarów D1 i D2 gdzie D1 jest od [0,1] i [x,2−y] i D2 [0,3] i [0,x]

Adam: up

Gray: Nie.

Adam: No dobra, to mógłbyś mi wytłumaczyć dlaczego w tym przykładzie mamy podzielony obszar na dwa http://i.imgur.com/wgYEkwF.jpg

Gray: Ten przykład z linku też można rozwiązać bez dzielenie na dwa. To powyższe z kolei też możesz podzielić na dwa (ale nie tak jak napisałeś). Ja pokazałem jak policzyć bez dzielenia. Mniej liczenia. Masz wybór.

Gray: Chcąc liczyć na dwie całki, musisz zrobić tak: I₁= ∫_[0,1] ∫_[0,x]xe^ydydx I₂=∫_[1,2] ∫_[0,2−x]xe^ydydx Twoja całka to I₁+I₂.

Adam: A jakby było z podzieleniem na dwa obszary ? Bo nie rozumiem tego twojego zapisu ∫[y,2−y] ∫[0,1] to wiem, że to przedział x

Adam: Rozumiem, ale nadal nie czaje tego zapisu ∫[y,2−y]

Gray: Zwróć uwagę na zamianę kolejności całkowania dxdy i dydx. W tym moim pierwszym wpisie, najpierw ustaliłem jak zmienia się y: od 0 do 1, potem, dla ustalonego y, jak zmienia się x: od y do 2−y. Stąd te przedziały. Obróć głowę o 90^o, aby to zobaczyć.

Adam: Ciężko mi to złapać, szkoda bo szybciej się liczy

Gray: Czego dokładnie nie możesz złapać? Jak zmienia się y w obrębie całego trójkąta? Patrzysz na poziome proste przecinające trójkąt. Od 0 do 1, tak?