Objętość figury obrotowej.
Draghan: Objętość figury.
W jakimś filmiku instruktażowym na YT znalazłem takie dwa wzorki na objętość bryły obrotowej,
powstałej z obrotu funkcji y = f(x) wokół osi:
a) OX: V = π ∫
ab y
2 dx
Co do tego wzoru nie mam żadnych zastrzeżeń, taki mam w książce, w zeszycie...
b) OY: V = π ∫
ab x
2 dy
Iiiiiii tutaj: w książce piszą, że wzorek dla osi OY to V = 2π ∫
ab xy dx
Czy wzór z filmu jest poprawny

Bo szczerze mówiąc − jest łatwiejszy do zapamiętania.

20 lut 02:09
Draghan: Już wiem, jaka jest różnica. We wzorze z filmu przedziałem całkowania były wartości na osi y.
Żeby ten wzór równał się książkowemu, musiałbym w książkowym za dolną granicę wstawić zero, a
za górną granicę − wartość x, wyliczoną ze wzoru funkcji dla igreka górnej granicy całkowania
ze wzoru z filmu.
Ale to pogmatwałem...

20 lut 02:24
Qulka: 
ale jak Ty wiesz to ok

20 lut 02:26
Qulka: bo już zaczęłam szukać Krysickiego

20 lut 02:27
Draghan: Zaraz machnę rysunki, żeby potomni wiedzieli...

20 lut 02:27
Draghan:
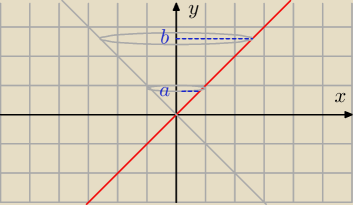
To byłaby figura wyliczona wg wzoru z filmu, dla
y = x i granic [a,b]...
20 lut 02:38
Draghan:
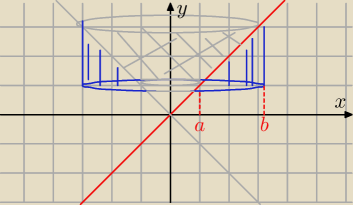
...a to byłaby figura dla wzoru "z książki", gdybym umiał tu rysować.

Wzór z filmu można uzyskać, jeśli odpowiednio ustalimy granice całkowania dla wzoru "z
książki".

20 lut 02:45
 Bo szczerze mówiąc − jest łatwiejszy do zapamiętania.
Bo szczerze mówiąc − jest łatwiejszy do zapamiętania. 

 ale jak Ty wiesz to ok
ale jak Ty wiesz to ok 


 To byłaby figura wyliczona wg wzoru z filmu, dla y = x i granic [a,b]...
To byłaby figura wyliczona wg wzoru z filmu, dla y = x i granic [a,b]...
 ...a to byłaby figura dla wzoru "z książki", gdybym umiał tu rysować.
...a to byłaby figura dla wzoru "z książki", gdybym umiał tu rysować.  Wzór z filmu można uzyskać, jeśli odpowiednio ustalimy granice całkowania dla wzoru "z
książki".
Wzór z filmu można uzyskać, jeśli odpowiednio ustalimy granice całkowania dla wzoru "z
książki". 