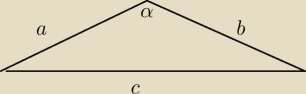
funkcje trygonometryczne w zadaniach geometrycznych numi: Dwa boki trójkąta mają długość a i b, kąt pomiędzy tymi bokami jest rozwarty, zaś pole trójkąta = 0,4ba, oblicz długość trzeciego boku tego trójkąta. Zupełnie nie mogę sobie z tym poradzić Obliczyłam kąt alfa, wyszło mi 126 stopni. Ale nie mam pojęcia co dalej zrobić, przekształcam wszystkie wzory, które znam i wciąż nie potrafię znaleźć niczego sensownego. Bardzo proszę o pomoc

rych: 0,5*a*b*sinα

rych: i tw cosinusow

Saizou :

	2		1
P=		ab=		absinα⇒{4}{5}=sinα
	5		2

	16		9		3		3
lcosαl=√1−sin2α=√1−		=√		=		⇒cosα=−		bo α jest rozwarty
	25		25		5		5

	6		6
c2=a2+b2−2abcosα=a2+b2+		ab⇒c=√a2+b2+		ab
	5		5

numi: Czyli tak to trzeba było zrobić! Już wszystko rozumiem, dzięki bardzo za pomoc