Wzajemne położenie dwóch okręgów. kqly: Z góry przepraszam że piszę w dwóch tematach. 1.Wyznacz równanie okręgu o najmniejszym promieniu, stycznego zewnętrznie do okręgu o: (x+3)²+y²=25 i jednocześnie stycznego do prostej k: 4x+3y−38=0. 2.Wyznacz równanie zbioru środków wszystkich okręgów zewnętrznie stycznych do okręgu o: x²+y²=4 i jednocześnie stycznych do prostej k: y+2=0.

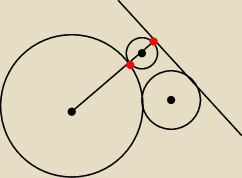
yolex: 1. Promień będzie najmniejszy, gdy środek leży na prostej prostopadłej do k i przechodzącej przez (−3,0) − środek danego okręgu. Każdy inny promień jest większy. Dlatego: 1. Piszesz równanie prostopadłej. 2. Rozwiązujesz układy: prostopadła + okrąg i prostopadła + dana prosta. Dostajesz dwa punkty (te czerwone). Srodek okręgu to środek odcinka a promień to odległośc pomiędzy środkiem a jednym z czerwonych.

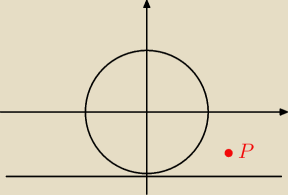
yolex: P(x,y). Wtedy odległość pomiędzy (0,0) a (x,y)=r+2 a odległość od P do prostej r=y−(−2) czyli y+2. Stąd √x²+y²=r+2 a r=y+2. √x²+y²=(y+4). Po podniesieniu obu stron do kwadratu i redukcji wyrazów podobnych dostajesz y=1/8x²−2. Jest to parabola, ale bez punktu (0,−2), bo wtedy nie ma okręgu − parabola jest styczna bezpośrednio do prostej i do danego okręgu, więc musiałby być promień=0

QWE: kqly ty cziterze xD

kqly: QWE ciąg się

yolex: Trochę ogłady by się przydało...

joxik: @yolex "KQLY" to Francuski, profesjonalny gracz gier komputerowych, zbanowany (zablokowano mu mozliwosc rozgrywek, brania udziału w turniejach etcetera), za oszukiwanie − z ang. (mocno spolszczone) cheatowanie. CHEAT − czytaj​ czit, cheater − cziter. Jak widac wyzej, zadania z matmy szukalo dwoch graczy/widzow rozgrywek gier komputerowych. Stad cala sytuacja. 'ciąg się' bylo zartem. TROCHE DOINFORMOWANIA, UMIEJĘTNEGO KORZYSTANIA Z GOOGLE to nie boli @yolex

Mu: Ale masz refleks− po 2 latach piszesz wyjaśnienie.