FUNKCJA KWADRATOWA Zdzisiu: Wyznacz wartości parametru m, dla których suma kwadratów dwóch różnych pierwiastków równania x²+(m+2)x+3m−2=0 jest większa od 7. Nie chce mi to wyjść. Co zrobiłem: 1) Założenia Δ>0, x1²+x2²>7 2) Δ=m²−8m+12>0 −−−> Δ_m=16 −−−> m1=2, m2=6 −−−−> m∊ (−∞;2) ∪ (6;∞) 3) x1²+x2²>7 −−−> (x1+x2)²−2x1x2>7 Ze wzorów Viete'a wyliczyłem: x1+x2=−m−2 x1x2=3m−2 4) (x1+x2)² − 2x1x2>7 I teraz jak to wyliczę, to wychodzi mi m1=−5+3√2, m2=−5−3√2, co nie zgadza się z wynikiem. Mógłby ktoś powiedzieć co jest źle?

Mila: Jaki masz wynik w odpowiedzi?

Zdzisiu: m∊(−∞;1) ∪ (1;2) ∪ (6;∞)

Mila: (x₁+x₂)²−2x₁*x₂>7 (m+2)²−2*(3m−2)>7 i Δ>0⇔ m²+4m+4−6m+4−7>0 i m∊ (−∞;2) ∪ (6;∞)⇔ m²−2m+1>0 (m−1)²>0⇔m≠1 i m∊ (−∞;2) ∪ (6;∞)⇔ m∊ (−∞;1)∪(1,2) ∪ (6;∞)⇔ Albo zapis z wyłączeniem 1 m∊ (−∞;2)\{1} ∪ (6;∞)

Zdzisiu: x1+x2 = −b/a czyli x1+x2=−m−2?

Zdzisiu: czy −m−2 to to samo co m+2?

Mila: Nie , to nie jest to samo, zauważ jednak, że: (−m−2)²=[(−1)*(m+2)]²=(−1)²*(m+2)²=(m+2)²

Zdzisiu: no tak, racja, dzięki

Zdzisiu: a mogłabyś mi jeszcze pomóc w tym przykładze: Wyznacz wartości parametru m, dla których kwadrat sumy dwóch różnych pierwiastów równania (4−m)x²+mx−m=0 jest większy od 1. Policzyłem Δ, z tego przedział m, potem znowu jak w poprzednim przykładzie w wzorów Viete'a itd. i doszedłem do momentu −2m³+8m²+16m−64>0? I nie mogę tego dalej wyliczyć, próbowałem schematem hornera, ale zostaje reszta i nic mi to nie daje, próbowałem rozbić, ale też mi sie nie udało

Zdzisiu: ?

Mila: W(m)=−2m³+8m²+16m−64 W(4)=−2*64+8*16+16*4−64=−128+128=0 Schemat Hornera: −2 8 16 −64 m=4 −2 0 16 0 −2m³+8m²+16m−64=(−2m²+16)*(m−4) licz dalej

Zdzisiu: a sprawdzałaś całość zadania? bo z pierwszego przedziału (tego z delty) wyszło mi m∊(−∞;0)∪(5 1/3;∞), teraz wyszło m1= √8 lub m1=−√8 i m2=4, a odpowiedź prawidłowa to m∊(2;4) ∪ 94;5 1/3). Skąd ta 2?

Zdzisiu: m∊(2;4) ∪ (4; 5 1/3) − prawidłowa odp

Mila: Nie sprawdzałam, założyłam, że masz problem z ostatnia nierównościa. zaraz sprawdzę.

Zdzisiu: no bo miałem też, ale wydawało mi się, że wszystko wcześniej było ok, a wynik znowu się nie zgadza

Mila: 1) m≠4

	16
2) Δ=−3m2+16m>0 dla m∊(0,4)∪(4,		)
	3

3) (x₁+x₂)²>1⇔

	m
(		)2>1⇔
	m−4

m2
	>1 /*(m−4)2
(m−4)2

m²>m²−8m+16⇔ m>2

	16
4) m∊(2,4)∪(4,		)
	3

Zdzisiu: Kolejny mój głupi błąd, dzięki wielkie, niepotrzebnie od (x1+x2)² odjąłem 2x1x2

Mila: Policzyłeś sumę kwadratów zamiast kwadrat sumy, dobrze, że teraz a nie na maturze. Teraz będziesz uważał.

Zdzisiu: Będę

Zdzisiu: Nie wychodzi mi kolejne zadanie tego typu: Wyznacz wartości parametru m, dla których suma odwrotności kwadratów dwóch różnych pierwiastków równania x²+2mx−x−1=0 jest równa 3. Δ>0 1/x1²+1/x2²=3 Δ=(2m−1)²+4=4m²−4m+5 I teraz Δ z m wychodzi ujemna?

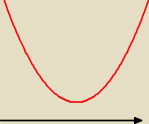
Czaruś: *Δ<0 oznacza, że nie ma miejsc zerowych (wykres nie przecina się z osią OX). a>0 a więc cała parabola znajduje się nad osią OX ⇒ m∊ℛ (dla dowolnego m: Δ>0) *patrząc na nierówność z innej strony: Δ>0 Δ= (2m−1)²+4 >0 (2m−1)² > −4 (dowolna liczba podniesiona do kwadratu jest nieujemna, a więc m jest dowolne (m∊R) ) Następnie robimy przekształcenie:

1		1
	+		=3
(x1)2		(x2)2

(x1)2+(x2)2		2x1x2
	=3 / +
(x1x2)2		(x1x2)2

(dzięki temu możemy licznik zwinąć: (a+b)²=a²+2ab+b² )

(x1+x2)2		2x1x2
	=3+		(*)
(x1x2)2		(x1x2)2

	c		−b
Teraz korzystamy ze wzorów Viete'a: x1x2=		oraz x1+x2=
	a		a

Otrzymujemy: x₁x₂=−1 x₁+x₂=1−2m Podstawiamy do (*):

(1−2m)2		−2
	=3+
(−1)2		(−1)2

(1−2m)2
	=1
(−1)2

( √a²=|a| ) |1−2m| = 1 1−2m=1 v 1−2m=−1 m=0 lub m=1