qqq
qaz: proste zadanko z pochodnej
| | 1 | |
Wyznacz maksymalne przedziały monotoniczności f(x)= |
| x4 − 2x3 + 5 |
| | 4 | |
f'(x)= x
3 − 6x
2 = x
2(x−6)
f'(x)>0
x∊(6,+
∞)
f'(x)<0
x∊ (−
∞,0)∪(0,6)
?
19 lut 16:34
J:
źle... w zerze jest odbicie
f'(x) >0 dla x ∊ (6,+∞)
f'(x) < 0 dla x ∊ (−∞,6)
19 lut 16:37
qaz:
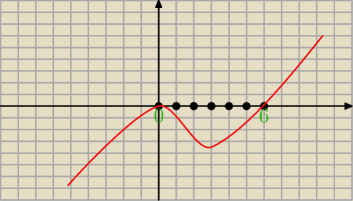
wiem,ale właśnie tego nie rozumiem...
tak wykres ma wyglądać?
19 lut 16:42
J:
tak ... to jest wykres pochodnej
19 lut 16:43
qaz: więc dlaczego mój przedział jest zły?
nie uwzględnia się zera jeśli jest w nim odbicie?
19 lut 16:47
J:
OK ... żle popatrzyłem na Twój przedział
masz dobrze
19 lut 16:48
qaz: hmmm... czyli Twój i mój przedział są prawidłowe? są takie same,ale inaczej zapisane?
19 lut 16:52
J:
nie , mój jest zły bo uwzględnił 0
19 lut 16:55
qaz: ehh... w odpowiedziach mam Twoje przedziały,do tego zamknięta (−
∞,6> i <6,+
∞)
19 lut 16:58
J:
no tak , mowa o maksymalnych przedziałach monotoniczności , stąd domknięte
19 lut 17:00
qaz: czyli Twoja odpowiedź jest jednak prawidłowa?
19 lut 17:05