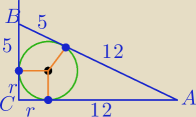
trójkąt opisany na okręgu seba: W trójkąt prostokątny wpisano okrąg. Punkt styczności okręgu dzieli przeciwprostokątną na odcinki o długościach 5 i 12. Oblicz pole trójkąta. Promień okręgu wyszedł √60 ale nie wiem czy dobrze

Mila: (5+r)²+(12+r)²=17², r>0 25+10r+r²+144+24r+r²=289 2r²+34r−120=0 r²+17r−60=0 Δ=289+240=529 √529=23

	−17−23		−17+23
r=		∉D lub r=		=3
	2		2

|AC|=12+3=15 |BC|=5+3=8 Spr. 8²+15²=64+225=289

	1
PΔ=		*8*15=60
	2

================

Mila: