zespolone wykresy modułów
Saris: |2iz+6|≤4
Jak dojść do nierówności koła? Rozpisywać z=x+iy do skutku?
18 lut 21:38
Lukas:
2|iz+6|≤4/2
|iz+6|≤2
|iz−6i2|≤2
|i(z−6i)|≤2
chyba jakoś tak
18 lut 21:43
Saris: Już ogarnąłem, ale
|2iz+6| = |2i| * |z+ 6/(2i)| = 2|z−3i| mógłby ktoś taką zależność bardziej rozpisać, nie widzę
ostatniego przejścia.
18 lut 21:55
ICSP: z = a + bi
|z| = √a2 + b2
|2i| = |0 + 2i| = √02 + 22 = √4 = 2
18 lut 21:56
Mila:
Skorzystamy z tego, że i2=−1 oraz |i|=1
|2iz+6|≤4 ⇔
2|iz+3|≤4 /:2
|iz−3i2|≤2
|i|*|z−3i|≤2⇔
|z−3i|≤2 koło o środku (0,3) i promieniu 2
18 lut 21:57
Gray: |z−3i|=|a+ib−3i|=|a+i(b−3)|=√a2+(b−3)2
18 lut 21:58
Saris: | | z | |
wydaję mi się, że to nie jest prawda i powinno być |
| w tym ostatnim module, bo chodzi |
| | −i | |
| | −i | |
chyba o to, że jest mnożenie |
| |
| | −i | |
18 lut 21:59
Saris: aaaa dzięki. Non stop zapominam, że to moduły liczb zespolonych i nie korzystam z tego.
18 lut 22:01
Saris: A w takim przykładzie:
|z+5|=|3i−z|
z1=−5
z2=3i
y=−5/3−8/3
Sprawdziłby ktoś?
18 lut 22:09
Saris: −5/3*x
18 lut 22:09
Saris: a coś takiego? |z+i|≤|z
2+i|. Wychodzi mi ciekawa nierówność uwikłana, to chyba nie tędy droga

.
18 lut 22:25
Saris: aa tam było +1

i wszystko jasne.
18 lut 22:40
Mila:
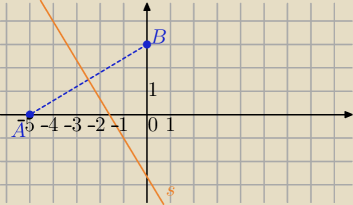
2)
|z+5|=|3i−z|⇔
|z−(−5)|=|z−3i|
interpratacja tego równania to symetralna odcinka
AB, gdzie A=(−5,0) i B=(0,3)
Możesz napisać to równanie mając końce odcinka albo z definicji modułu
z=x+iy
|x+iy+5|=|3i−x−iy|
|(x+5)+iy|=|−x+i*(3−y)|⇔
(x+5)
2+y
2=x
2+(3−y)
2⇔po przekształceniach:
===============
18 lut 22:46
Mila:
3)
|z+i|≤|z2+1| tak?
18 lut 22:47
kyrtap: |z+i|≤|(z−i)(z+i)|
|z+i|≤|z−i|*|z+i| /: |z+i|
1≤|z−i|
18 lut 23:01
Saris: tak już doszedłem do tego

, ale dzięki.
18 lut 23:03
Mila:
Patryk nie dzielisz, bo gubisz rozwiązanie, przenosisz na jedna stronę, a potem wyłączasz
wspólny czynnik.
Popraw, dobrze zacząłeś.
18 lut 23:03
kyrtap: |z+i| −|z−i|*|z+i|≤0
|z+i|(1 − |z−i|)≤0 i teraz Mila będą dwa przypadki wtedy kiedy jedno wyrażenie będzie mniejsze
od zera a drugie większe i na odwrót czy się mylę?
18 lut 23:11
Saris: | | |z+i| | |
ten przykład wyglądał tak: |
| ≤1 (z≠i, z≠−i) tak w ogóle. W takim przypadku |
| | |z2+1| | |
można dzielić, jakby od początku wyglądał tak jak go podałem to nie

18 lut 23:17
Saris: moduł jest zawsze dodatni, więc rozwiązujesz to co jest w nawiasie.
18 lut 23:20
Saris: znaczy kiedy jest ≤0
moduł jest zawsze nieujemny*
18 lut 23:21
Mila:
No to narysujcie ten zbiór punktów Panowie.
18 lut 23:26
kyrtap: ja Milu wrócę do tego jutro rano, dzisiaj nie mam weny
18 lut 23:34
Mila:
Dobrze, też mam słabą formę.
Dobranoc.
18 lut 23:46
kyrtap: 
19 lut 00:28
Saris:
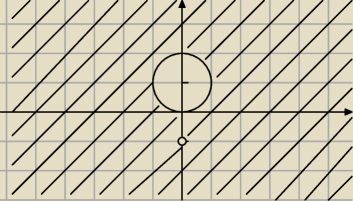
coś takiego, nie za dobry jestem w rysowaniu

.
19 lut 00:44
Saris: a ja mam takie pytanko:
|z− +2−i|≤|z|
z− − sprzężenie z
wiadomo, że rozwiązanie półpłaszczyzna, której elementy są bardziej odległe od z1=0 oraz (no
właśnie) z2=−2−i. Czemu? sprzężenie to po prostu odbicie względem osi Re, więc jeśli mamy
|z− +2−i|=|z− −(−2+i)| to punkt odbicie punktu (−2,1) to ten nasz szukany z2, ale jak to
wykazać algebraicznie? Wyprowadzić liczbę z bez sprzężenia?
19 lut 00:51
Saris: nie oraz tam ma być tylko niż od z2
19 lut 00:51
Saris:
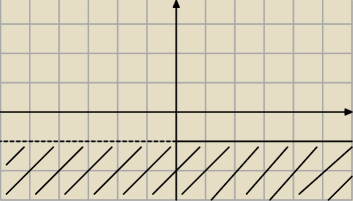
| | 1 | |
kolejne pytano: wykres arg( |
| )<π, będzie wyglądał jak wyżej? |
| | z+i | |
W odopowiedziach mam odwrotnie, zaznaczone jest to góry, ale według mnie tak by wyglądał z+i.
obraz 1/z wyglada tak samo jak sprzężenie z, więc nie wiem czy ja źle rozumuje czy błąd w
odpowiedziach.
19 lut 02:42
Gray: A co to jest arg? Argument, czy argument główny? Jeżeli argument, to zadanie jest mało
sensowne. Jeżeli argument główny to pojawia się kolejne pytanie: jak miałeś zdefiniowany
argument główny?
Jeżeli był to kąt z przedziału (0,2π] spełniając wiadome warunki to Twój obszar wyznaczasz tak:
| | 1 | |
0≤arg( |
| )<π ⇔ 0≤ −arg(z+i) + 2kπ<π ⇔ 2kπ≥arg(z+i)>−π+2kπ. |
| | z+i | |
Aby zmieścić się w przedziale (0,2π] należy przyjąć k=1:
2π≥arg(z+i)>π.
Wygląd więc na to, że masz dobrze.
19 lut 09:30
Saris: treść brzmiała narysować zbiór liczb zespolonych, które spełniają podane warunki.
Dziękuje.
a ktoś ma odp. do wcześniejszego pytania?
19 lut 10:29
Saris: albo przykład:
arg(−z)=argz+π dla 0≤argz<π
argz−π dla π≤argz<2π
| π | |
| ≤arg(−z−(−i−2))=arg(z−(i+2)+π≤π |
| 6 | |
dobrze?
19 lut 10:37
Saris: mam taki dylemat.
Mam przedstawić liczbę w postaci trygonometrycznej:
z=4−i
|z|=
√17
sinφ=nic fajnego (−) IV ćw.
cosφ=nic fajnego (+)
| | 1 | | 1 | |
z=√17(cos(2π−arctg |
| )+i*sin(2π−arctg |
| )) tak jest też w odpowiedziach |
| | 4 | | 4 | |
ale dla:
z=−2+i
|z|=
√5
sinφ=nic fajnego (+) II ćw.
cosφ=nic fajnego (−)
| | −1 | | 1 | |
φ=arctg |
| +π=π−arctg |
| (a<0) |
| | 2 | | 2 | |
| | 1 | | 1 | |
z=√17(cos(π−arctg |
| )+i*sin(π−arctg |
| )) tak jest w odpowiedziach. |
| | 2 | | 2 | |
| | 1 | | 1 | |
Tyle, że to jest II ćw, więc moim zdaniem powinno być φ=π−(π−arctg |
| )=arctg |
| |
| | 2 | | 2 | |
W odpowiedziach jest źle, czy ja źle myślę? W 1 przykładzie korzystam z tych reguł na ćwiartki,
a w tym już nie. Dlaczego?
19 lut 11:27
Gray: | | −1 | |
Skąd wziąłeś to π: φ=arctg |
| +π ? |
| | 2 | |
19 lut 11:34
19 lut 11:43
Gray: To albo dodajesz tu, albo później (we wzorze na postać tryg.); a nie tu i tu. Dodanie π ma cię
przenieść do właściwej ćwiartki.
19 lut 11:46
Saris: Jakby ktoś mi pomógł z 00:51 i 10:37 byłbym też bardzo wdzięczny.
19 lut 11:47
Saris: To ten wzór działa tak:
I ćw. a>0, b>0
nic nie dodaje φ=arctg(b/a)
II ćw. a<0, b>0
ze wzoru (znowu nic nie dodaje): π+arctg(b/a) = π−arctg(|b/a|)
III ćw. a<0. b<0
ze wzoru (znowu nic nie dodaje): π+arctg(b/a)
IV ćw. a>0. b<0:
ze wzoru mam nic nie dodawać: arctg(b/a)=−arctg(|b/a|)=2π−arctg(|b/a|)
19 lut 11:56
Saris: ?
19 lut 11:57
Saris: chodzi, mi o to, że nie dodaje czyli już nie patrzę na ćwiartki.
19 lut 11:57
Gray: | | Rez | |
Ja wolę inaczej na to popatrzeć. Wyznaczam φ=arctg |
| i dodaję odpowiednie kąty dopiero |
| | Imz | |
w postaci trygonometrycznej. To φ oczywiście nie musi być argumentem liczby zespolonej z.
19 lut 12:06
Saris: znaczy ja używam tego wzoru, tylko jeśli układ jest nie wyliczalny bez tablic/kalkulatora, żeby
zachować dokładność.
Jest jakiś sposób, żeby od razu wiedzieć jak podejść zadanie typu przedstawienie
iloczynu/ilorazu liczb zespolonych w postaci trygonometrycznej? Chodzi mi o to, że przykład
może być zadany w taki sposób, że policzymy tylko wtedy jeśli przekształcimy liczby osobno i
podstawimy do wzoru, a innym razem obydwie nie wyjdą dopóki pierw nie przemnożymy
algebraicznie (albo podzielimy w przypadku ilorazu). Co jeśli w obu przypadkach będzie
wychodzić coś nie do policzenia? Przedstawić to wtedy jako sumę/różnicę tych arcusów ze
wzoru(chodzi mi o kąt) czy da się to jakoś obejść, tak żeby zachować dokładność.
19 lut 12:20
Gray: Regułą jest tu brak reguły.
19 lut 12:51
Saris: z3=−z−
zaciąłem się.
19 lut 12:54
Gray: Z postaci trygonometrycznej...
19 lut 13:01
Saris: |z|3*(cos3φ+i*sin3φ)=|z|(cosφ+i*sinφ)
|z|2*(cos3φ+i*sin3φ)=(cosφ+i*sinφ)
ale tu z tymi kątami będzie jakiś meksyk... 4 przypadki?
19 lut 13:24
Saris: one teraz są źle zapisane.
19 lut 13:24
Saris: ktoś pomoże?
19 lut 13:42
Saris: jednak mi się udało.
19 lut 14:01
Saris: z3=−8i
|z|3*(cos3φ+isin3φ)=8(cos(3π/2)+isin(3π/2))
|z|=2
φ2=3π/2
rozpatruje 4 przypadki (3φ, 3π−1φ, 3π+3φ, −3φ), mam z nich 2 rozwiązania, a okazuje się, że
rozwiązaniem jest tylko 2i (−2i już nie), a 2 inne rozwiązania wychodzą z kąta φ2=−π/2 i też
muszę z 4 wybrać tylko 2.
Jak mam to ograniczyć... Czemu, muszę brać różne kąty..
19 lut 14:34
Gray: To może ten ostatni przykład. Robimy tak
|z|3(cos3α+isin3α)=8(cos3π/2)+isin(3π/2)).
Teraz najważniejsze: liczby zapisane w postaci trygonometrycznej są równe, gdy mają te same
moduły (czyli |z|3=8) a ich argumenty różnią się całkowitą wielokrotność 2π (czyli 3α=3π/2
+2kπ).
Stąd
|z|3=8 ⇔ |z|=2
oraz
3α=3π/2 +2kπ ⇔ α=π/2 + 2kπ/3.
Musimy wybrać te k, które dadzą różne rozwiązania: widać, że to będzie k=0,1,2.
Stąd Twoje rozwiązania to:
zk=2(cos(π/2 + 2kπ/3)+isin(π/2 + 2kπ/3)), dla k=0,1,2.
19 lut 14:50
Saris: o super. Dzięki. Teraz widzę o co chodzi.
19 lut 15:00
Saris: z=wn − gdzie w to pierwiastek.
Korzystając z tego wzoru wyliczyć pierwiastki zbioru:
√−7+24i
w odp. są ładne liczby, a ja to policzyłem korzystając z arcusów, bo nic ładnego nie
wychodziło... Postać zespolona dowolna.
Błąd w odpowiedziach czy rzeczywiście ładnie się to liczy? Nie mogłem wyliczyć kąta fi. z
układu sincos
19 lut 18:06
Saris: Rzeczywiście ładne wyniki wychodzą to nie rozumiem.
w2=−7+24i
w2=25(cosφ+i*sinφ)
sinφ=24/25
cosφ=−7/25
...
19 lut 18:11
Saris: Ok, już rozumiem, wcale tu nie korzystam z definicji.
19 lut 18:13
Saris: 4√−1
w=(x+yi)4=x4+4x3yi−6x2y2−4xy3i+y4
−1=x4+y4−6x2y2
0=43y−4y3
Rozwiązałem to, ale wyszły błędne wyniki. Jakaś wskazówka?
19 lut 18:37
Gray: Jest wzór na pierwiastki algebraiczne z liczby zespolonej.
Rozwiązaniami równania z
n=c są liczby
| | α+2kπ | | α+2kπ | |
zk=n√|c|(cos |
| +isin |
| ), k=0,1,...,n−1, |
| | n | | n | |
gdzie α=argc.
4√−1 to rozwiązania równania z
4=−1.
19 lut 18:53
Gray: Kiedyś rozwiązywałem równanie w2=−7+24i korzystając z postaci trygonometrycznej − da się bez
znajomości kąta φ. Należy skorzystać ze wzoru, który podałem Ci wyżej.
19 lut 18:56
Saris: właśnie w tym zadaniu chodzi o to, żeby nie korzystać ze wzoru na pierwiastki.
To w2=−7+24i właśnie robiłem z tego wzoru nie licząc bezpośrednie kąta, tylko używając arctg,
ale wynik jest strasznie brzydki, a z tych układów równań wyszedł ładny.
Za to 4√−1 zrobiłem z tego wzoru i wyszło wszystko łądnie, ale z układów np. już nie
wychodziło.
Teraz robię:
3√−2−2i i nie idzie ani ze wzoru ani z układów, znaczy ze wzorów też mogę policzyć arctg i
zapisać to, ale wiem, że wynik ma być ładny, więc jakoś się inaczej da.
19 lut 19:13
Gray: W tym z w2 można uzyskać ładne rozwiązania bez arctg; wystarczy sprytnie skorzystać ze wzorów
na sin2x i cos2x.
19 lut 19:17
Saris: jakiś pomysł do tego −2−2i?
19 lut 19:24
MQ: −2−2i=2√2ei3π/2
i pierwiastkujesz
19 lut 19:27
MQ: Źle, powinno być:
2√2ei5π/4
19 lut 19:28
Saris: no ale to ja wiem

a z drugiej strony będzie:
|w|
3*e
i3φ
3φ=5π/4+2kπ
φ=5π/12+2kπ/3
i lipton, nie wiem jak to wyprostować.
19 lut 19:33
MQ: No i masz już policzone. Czego jeszcze chcesz?
19 lut 19:52
Saris: tego, że takich kątów sie nie da policzyć, a wychodzą skończone liczby bez żadnych funkcji w
odp.
19 lut 20:12
MQ: Jakich kątów nie da się policzyć?
Przecież masz policzone kąty. Sam je podałeś!
19 lut 20:16
Saris: nie kątów tylko wartości fukncji tryg.
19 lut 20:28
MQ: A po kiego grzyba ci to potrzebne? Wynik masz w eleganckiej postaci eksponencjalnej

, a jak
ci nie pasuje, to przejdź na postać trygonometryczną

i już.
19 lut 20:37
MQ: A jak tak się upierasz, to skorzystaj z takich tożsamości:
1. 5π/12= π/2−π/12
2. π/12=(π/6)/2
sin π/6 znasz
cos π/6 znasz
teraz liczysz sin π/12 i cos π/12 z 2.
a potem
sin 5π/12 i cos 5π/12 z 1.
z kolejnymi kątami podobnie.
19 lut 20:43
Saris: Dzięki.
taki przykład:
(z−i)4=(iz+3)4
z−i=iz+3 ⇒ z0=2i+1
Teraz chciałem przemnażać przez (cos2kπ/4+isin2kπ/4), ale wychodzą w ogóle złe pierwiastki,
czemu?
Doszedłem jeszcze do tego, że jeśli tam jest potęga stopnia 4, to można odwrócić różnicę z−i na
i−z i wtedy wychodzi drugi pierwiastek −1+2i.
W odpowiadziach mam jeszcze 1, tzn, że jest dwukrotny tak? Jednak nie umiem go znaleźć, nie
wiem czemu mnożenie przez (cos2kπ/4+isin2kπ/4) nic nie daje w tym wypadku.
19 lut 21:13
Gray: A czemu miałoby coś dawać? Można sobie tak domnażać dla równania postaci zn=c. Twoje takie nie
jest.
Możesz poradzić sobie tak: (z−i)4=(iz+3)4 ⇔(z−i)4−(iz+3)4=0 ⇔ ... a2−b2=(a−b)(a+b)..
Dalej Ty.
Jeszcze jedno: odnoszę wrażenie, że myślisz, że to równanie ma cztery rozwiązania. Dlaczego?
19 lut 21:19
Saris: hmmm, bo jest 4 potęga, tak mi się wydawało.
19 lut 21:21
Gray: A takie równanie ile ma rozwiązań: z4=z4−z+1 ?
19 lut 21:22
Saris: no wiem o co chodzi, głupio pomyślałem.

Zrobiłem już z wzoru skróconego mnożenia dzięki.
19 lut 21:28
Saris: Zostało mi ostatnie, ale z gwiazdką.
(z+1)6+z6=0
Zapewne też jakoś się to poskraca.
19 lut 21:32
Gray: To zrobiłbym tak:
(z+1)
6+z
6=0 ⇔ (z+1)
6=−z
6 ⇔ ... z=0 nie jest rozwiązaniem, więc mogę podzielić stronami
przez z
6... ⇔ ((z+1)/z)
6=−1.
Wystarczy więc obliczyć
6√−1. To są liczby
| | π+2kπ | | π+2kπ | |
ek=cos |
| +isin |
| , dla k=0,1,2,3,4,5 |
| | 6 | | 6 | |
Stąd
| | 1 | | 1 | |
(zk+1)/zk=ek ⇔ zk = |
| = |
| , dla k=0,1,...,5. |
| | ek−1 | | | | π+2kπ | | π+2kπ | | cos |
| +isin |
| −1 | | | 6 | | 6 | |
| |
Koniec.
19 lut 21:54
Saris: (7i−z)3=(1+2i)6
z0=3i+3
jak to rozbić dalej?
20 lut 11:30
Saris: .
20 lut 12:51
Saris: .
21 lut 17:36
Gray: Rozwiązania równania zn=c to wierzchołki n−kąta foremnego wpisanego w okrąg o promieniu
n√|c| − to fundamentalny fakt przy rozwiązywaniu tego typu równań.
Wykorzystując go mamy:
7i−z0=(1+2i)2 = −3 + 4i
7i−z1=(−3+4i)(cos(2π/3)+isin2π/3)=... dolicz sam
7i−z2=(−3+4i)(cos4π/3+isin4π/3)=... dolicz sam.
Stąd:
z0=3+3i
z1=7i−(−3+4i)(cos(2π/3)+isin2π/3)
z2=7i−(−3+4i)(cos4π/3+isin4π/3)
21 lut 18:49
Saris: a czyli jednak tak jak myślałem. Dzięki.
21 lut 18:53
 .
.
 i wszystko jasne.
i wszystko jasne.
 2)
|z+5|=|3i−z|⇔
|z−(−5)|=|z−3i|
interpratacja tego równania to symetralna odcinka
AB, gdzie A=(−5,0) i B=(0,3)
Możesz napisać to równanie mając końce odcinka albo z definicji modułu
z=x+iy
|x+iy+5|=|3i−x−iy|
|(x+5)+iy|=|−x+i*(3−y)|⇔
(x+5)2+y2=x2+(3−y)2⇔po przekształceniach:
2)
|z+5|=|3i−z|⇔
|z−(−5)|=|z−3i|
interpratacja tego równania to symetralna odcinka
AB, gdzie A=(−5,0) i B=(0,3)
Możesz napisać to równanie mając końce odcinka albo z definicji modułu
z=x+iy
|x+iy+5|=|3i−x−iy|
|(x+5)+iy|=|−x+i*(3−y)|⇔
(x+5)2+y2=x2+(3−y)2⇔po przekształceniach:
 , ale dzięki.
, ale dzięki.


 coś takiego, nie za dobry jestem w rysowaniu
coś takiego, nie za dobry jestem w rysowaniu  .
.

 a z drugiej strony będzie:
|w|3*ei3φ
3φ=5π/4+2kπ
φ=5π/12+2kπ/3
i lipton, nie wiem jak to wyprostować.
a z drugiej strony będzie:
|w|3*ei3φ
3φ=5π/4+2kπ
φ=5π/12+2kπ/3
i lipton, nie wiem jak to wyprostować.
 , a jak
ci nie pasuje, to przejdź na postać trygonometryczną
, a jak
ci nie pasuje, to przejdź na postać trygonometryczną  i już.
i już.
 Zrobiłem już z wzoru skróconego mnożenia dzięki.
Zrobiłem już z wzoru skróconego mnożenia dzięki.