rozwiązanie do dowodu w trygonometrii - sprawdzenie Michał: Witam, Mam problem z zadaniem. Nie wiem czy moje rozwiązanie jest poprawne. Oto treść: Udowodnij, że równanie nie ma rozwiązań.

	π
cos2xsinx+√3sin2x+2sinx=3tg
	3

No i moje rozwiązanie jest bardzo na logikę, ale też bardzo, ale to bardzo nieprecyzyjne. cos²x − maksymalna wartość to 1 sinx − maksymalna wartość to 1 √3sin²x − maksymalna wartość to √3 2sinx − maksymalna wartość to 2 Nawet, jeśli składowe tej funckji osiągałyby maksima przy tej samej odciętej, to: 1+1+√3+2=3+√3 < 3√3

	π
uzyskiwana przez nie wartość jest mniejsza od wartości 3tg		.
	3

Czy takie rozwiązanie jest poprawne i czy zostałoby uznane na maturze? Jeśli ktoś ma na nie inny pomysł, to proszę o przedstawienie go. Pozdrawiam

Eve: ja bym jednak rozpisała to w innej formie: (1−sin²x)sin²x+√3sin²x+2sinx=sin²x−sin³x+√3sinx+2sinx=−sin³x+√3sin²x+3sinx

prosta: podstawić za sinx zmienną...przy łożeniu, że t∊<−1,1>

Michał: ale rozwiązanie będzie takiego typu jak ja pokazałem, czy coś jeszcze trzeba z tym dalej zrobić? Bo najpierw zabrałem się za to, tak jak ty @Eve , ale nie potrafiłem potem nic z tym zrobić.

Eve: potem faktycznie mozna sprawdzić wartości w granicach przedziału

Michał: Czyli jest ok, czy zrobiłabyś/zrobiłbyś to inaczej?

Eve: to wystarczy, chociaż, dla t=√3 faktycznie lewa strona przyjmuje wartość 3p{3, ale sinα nie może przyjmować takiej wartości√3

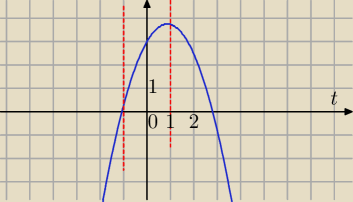
Mila: Przekształcam równanie do postaci: sinx*(−sin²x+√3sinx+3)=3√3 g(x)=−sin²x+√3sinx+3 sinx=t g(t)=−t²+√3{t}+3, t∊<−1,1> badam zbiór wartości g(t)

	−√3		√3
tw=		=		∊<−1,1>⇔
	−2		2

	√3
g(t) ma największą wartość dla t=
	2

	√3		15
g(		)=
	2		4

Wartość najmniejsza g(t): g(−1)=−1−√3+3=2−√3

	15
2−√3≤−sin2x+√3sinx+3≤
	4

15		225
	<3√3 ( bo		<27 porównuję kwadraty liczb)
4		16

Dalej możesz łatwo dokończyc uzasadnienie. Posprawdzaj rachunki

Michał: Aaaaaa, to takie to proste było. Dziękuję ślicznie

Mila:

Eta:

	π
..... tg		=√3
	3

cos²xsinx+2sinx+√3sin²x−3√3=0 sinx(cos²x+2)−√3(3−sin²x))=0 sinx(3−sin²x)−√3(3−sin²x)=0 (3−sin²x)(sinx−3)=0 ⇒ (√3−sinx)(√3+sinx)(sinx−3)=0 −−−−−−− brak rozwiązań

Eta: Poprawię jeszcze chochlika (3−sin²x)(sinx−√3)=0

Mila: Hej, ładnie.

Eta: