Geometria analityczna - odległość punktu od prostej Kuba: Wyznacz równanie prostej zawierającej dwusieczną kąta utworzonego przez proste k: x+3y−1= 0 m: 6x−2y+1 = 0 do obszaru którego należy punkt P=(3;1). Ze wzoru na odległość punktu od prostej obliczyłem dwie możliwości równania prostej będącej dwusieczną kąta − n: (4x−8y+3 = 0 ∨8x+4y−1 = 0). Moje pytanie brzmi: w jaki sposób sprawdzić, która z tych prostych dzieli kąt zawierający podany punkt P?

Eve: podstaw współrzędne P do równania prostej

Kuba: Próbowałem − nie działa. Poza tym, to chyba nie jest w pełni zgodne z treścią polecenia, gdzie mowa jest o obszarze kąta, niekoniecznie punkcie należącym do prostej.

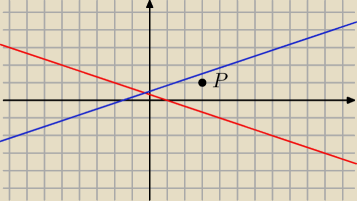
Eve: tak to wygląda, chyba masz złe proste

Kuba: Sprawdziłem właśnie odpowiedź i myślę, że proste są w porzadku, bo jedna z nich występuje jako odpowiedź prawidłowa (4x−8y+3 = 0).

Eve: jesli tak, to w drugiej masz złe znaki wyznacz w tych prostych y

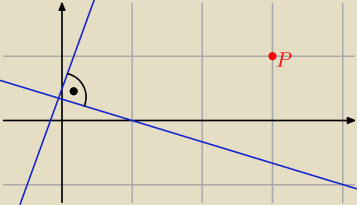
Bogdan: Warto zauważyć, że proste są prostopadłe

Eve: z rysunku też mi tak wyszło, ale nie chciało mi się sprawdzać rachunkiem

Bogdan:

	1		1
k: y = −		x +
	3		3

	1
m: y = 3x +
	2

	1
−		*3 = −1 ⇒ k⊥m
	3

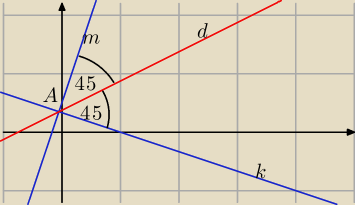
Bogdan: d − dwusieczna, d: y = ax + b

	−1
współczynniki kierunkowe: am = 3, ak =		,
	3

	1		7
proste m i k przecinają się w punkcie A = (−		,		,
	20		20

kąt między dwusieczną i prostą m oraz między dwusieczną i prostą k ma miarę 45^o tg45^o = 1 Korzystamy z wzoru na tg kąta między prostymi

	am − a		3 − a		1
tg45o =		⇒ 1 =		⇒ a =
	1 + am*a		1 + 3a		2

	1		1		7		3
dwusieczna d: y =		(x +		) +		⇒ y = U{1}[2}x +
	2		20		20		8

Bogdan:

	1		3
d: y =		x +
	2		8