proszę o pomoc paulina: Mając dany ostrosłup prawidłowy czworokątny, w którym kąt płaski ściany bocznej przy wierzchołku ostrosłupa jest przystający do kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy, wyznacz cosinus tego kąta oraz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. Bardzo proszę o pomoc

paulina: ponawiam prośbę...

paulina: ma ktoś jakiś pomysł?

prosta: wypadałoby ustalić ile jest równy stosunek a/k....stosunek krawędzi podstawy do krawędzi bocznej Zapisałam dwa związki: na cosα w trójkącie prostokątnym i z tw,. cosinusów dla kąta przy wierzchołku ostrosłupa. wstawiając cosα z 1 do 2 mam związek między a i k. Można wyznaczyć iloraz a/k ( z powstałego równania kwadratowego)...tylko liczby brzydie, jakieś

prosta:

	1+√5
otrzymuję:cosα=
	2

prosta:

	a√2
1. cosα=		2. a2=k2+k2−2k2cosα
	2k

	a√2
a2=2k2−2k2
	2k

a²=2k²−ak√2 /:k²

	a		a
(		)2=2−(		)√2
	k		k

	a		√2−√2
po obliczeniu:		=
	k		2

Bogdan: √2 − √2 = 0 ?

prosta:

√2−√10
2

prosta:

	a		−√2+√10
ups:		=
	k		2

	√2		−√2+√10		−1+√5
cosα=				=
	2		2		2

teraz to ma sens

Bogdan:

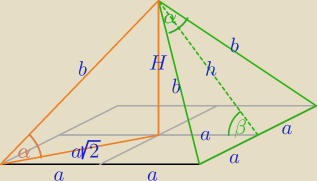
	a√2		2b2 − 4a2		a
cosα =		i cosα =		= 1 − 2(		)2 = 1 − cos2α
	b		2b2		b

	π
cos2α + cosα − 1 = 0 cosα ∊ (0,		)
	2

prosta: jak można taki ładny szkic wyrysować?

prosta:

	π
cosα>0 bo α∊(0,		)
	2