Zadanie opisowe
Początkujący matematyk: Cześć! Z cyklu troszkę innych, ale trudnych, zadanek: Turysta obserwuje z wysokości 300 m
n.p.m. szczyt pod kątem 40*. Po podejściu w stronę wzniesienia o 500 m po stoku o nachyleniu
10*, kąt pod którym obserwuje szczyt wyniósł 60*. Jakiej wysokości jest wzniesienie?
* − stopni
Wieeelkie dzięki z góry

17 lut 19:50
PW: Chyba pod górę. Panie Kolego, symbol stopnia uzyskuje się wklepując Alt0176 z klawiatury
numerycznej przy włączonym NumLock
17 lut 19:59
Początkujący matematyk: Jestem na ipadzie

Pomógłbyś mi bardziej gdybyś jakoś wskazał jak rozwiązać zadanko

Ale przynajmniej teraz wiem coś nowego, dzięxy

17 lut 20:07
PW: Oj, tego nie umiem. Deprymuje mnie to morze i jeszcze 300 m npm. Zaczynam podejrzewać, że góra
rośnie w morzu.
17 lut 20:15
Eve:
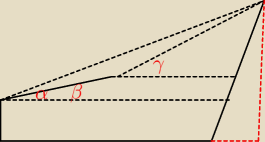
17 lut 20:21
Początkujący matematyk: Ja to bym chętnie to wszystko skminił, ale sam nie potrafię. Gdybyś EVE mógł/a mi jakoś pomóc,
byłoby git (y) − nie wykluczam pik niku w parku łazienkowskim

17 lut 20:27
Bogdan:
a wzrost turysty zalicza się do tych 300 m?, przecież turysta jak sądzę obserwuje szczyt
nie leżąc z okiem przy gruncie

17 lut 20:30
Eve:
no to wyszło mi tak:
z=500sin10
y=500cos10
H=x
√3+300
17 lut 20:33
Początkujący matematyk: Myślę, iż trzeba przyjąć, że poprostu z 300 m − np. chilluje leżąc z tym okiem przy gruncie. No
słuchaj, to nie ja wymyśliłem te zadanie tylko mam je z książki i poprostu przepisałem.
17 lut 20:34
Początkujący matematyk: Hola hola, powolutku. To wszystko? W sensie nie ma więcej obliczeń? Albo może gdybyś mi mogła
tak troszkę lepiej wytłumaczyć...
17 lut 20:36
Eve: wstaw do tg40 za z i y, oblicz x
17 lut 20:40
Eve: wyszło mi, że wysokość wzniesienia ok 666m − no co za liczba

17 lut 20:47
PW: Zaiste, szatański to pomysł. Użyłaś tej liczby 300 m npm. do rozwiązania?
17 lut 21:32
Eve: tak

17 lut 22:14

 Pomógłbyś mi bardziej gdybyś jakoś wskazał jak rozwiązać zadanko
Pomógłbyś mi bardziej gdybyś jakoś wskazał jak rozwiązać zadanko  Ale przynajmniej teraz wiem coś nowego, dzięxy
Ale przynajmniej teraz wiem coś nowego, dzięxy 




