Okrąg a prosta Pokażmihontas: Witam, mam problem w zadaniu: Oblicz najmniejszą odległość pomiędzy okręgiem o równaniu x²−4x+4y+y²+4=0 a prostą 2x+2−y=0. Dziękuję z góry

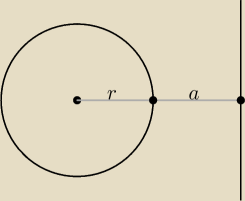
Bogdan: Środek okręgu S = (2, −2), długość jego promienia r = √4 + 4 − 4 = 2 Odległość od S do prostej: d = ..., najmniejsza odległość od tej prostej do okręgu jest równa a = ... (i uruchamiamy myślenie)

PW: Odległość między zbiorami to najmniejsza odległość między dowolnym punktem jednego ze zbiorów a dowolnym punktem drugiego ze zbiorów (a jeśli nie istnieje najmniejsza, to kres dolny). Odległość między zbiorami jest więc liczbą. Nie ma czegoś takiego jak "najmniejsza odległość między zbiorami". Pytanie jest bez sensu.

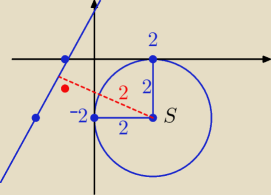
Janek191:: ( x − 2)² − 4 + ( y + 2)² − 4 + 4 = 0 ( x − 2)² + ( y + 2)² = 2² S =( 2 ; − 2) r = 2 oraz y = 2 x + 2 2 x − y + 2 = 0 Obliczam odległość punktu S od danej prostej

	I 2*2 + (−1)*(−2) + 2I		8
d1 =		=
	√22 + 1		√5

zatem szukana odległość

	8
d = d1− r =		− 2
	√5

===================

Pokażmihontas: Dzięki Janek191 i Bogdan. PW, myślisz, że powinnam tak napisać na sprawdzianie?

PW: Tak, ja postawiłbym Ci szóstkę za dokładne rozumienie teorii (a sam stuknął się w łeb, co wypisuję w treści zadania).