Funkcja kwadratowa z parametrem/wartość bezwzględna Marysia: Dla jakich m równanie |x²−6x|=m ma co najmniej trzy rozwiązania. Jak dla mnie jest to możliwe tylko w przypadku stałej funkcji liniowej y=[jakaś liczba] czyli w tym przypadku musiałoby być y=0, ale nie wiem czy dobrze rozumuję, dlatego proszę o rozwiązanie tego zadania.

Tadeusz:

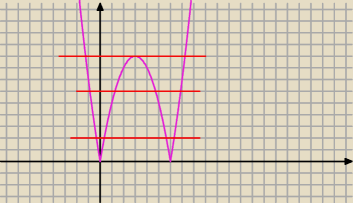
Tadeusz: −Narysuj wykres y=|x²−6| −"tnij" go stałą y=m −wnioskuj

pigor: ..., niestety źle rozumujesz : najlepiej zrób sobie wykres paraboli pod modułem : f(x)=|x²−6x|= |x(x−6)| i p=¹₂(0+6)= 3 , to |f(3)| = |−9| = 9 , a wtedy prosta y=m równoległa do Ox przecina wykres funkcji f w 3−ech albo 4−ech punktach ⇔ 0< m ≤ 9 ⇔ m∊(0 ;9> . ..

Marysia: Jasna sprawa, teraz wydaje się to takie banalne, że aż mi wstyd.. Dziękuję bardzo panowie. Przy okazji mam kolejne pytanie odnośnie założeń w tym zadaniu: Dla jakich wartości parametru m trójmian kwadratowy f(x) = (m−1)x ² + 2mx+3m−2 jest kwadratem pewnego dwumianu? 1) Δ=0 2) m−1>0 Dlaczego tutaj nie wystarczy sam warunek m≠1?

Marysia: Czy potrafi ktoś w łatwy sposób wyjaśnić?

zombi: Bo ma być kwadratem, czyli przed x² musi być liczba dodatnia, bo jak podnosisz dwumian do kwadratu to nie otrzymasz przez x² nigdzie minusa.