Geometria analityczna z analizą Razor3: Prosta l przecina dodatnie półosie układu współrzędnych w punktach A i B. Wyznacz równanie tej prostej jeżeli |AB|=6√2 i obwód trójkąta ABO jest największy. O(0,0) Czy to zadanie da się zrobić tylko za pomocą pochodnych?

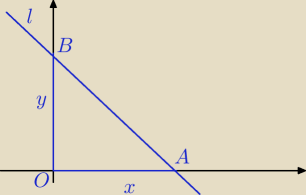
Janek191:: x > 0 i y > 0 I AB I = 6√2 A = ( x , 0) B = ( 0, y) oraz x² + y² = ( 6√2)² = 72 ⇒ y² = 72 − x² ⇒ y = √72 − x² Obwód Δ ABO L = x + y + 6√2 = x + √72 − x² + 6√2 L(x) = x + √ 72 − x² + 6√2 więc

	− 2 x		x
L '(x) = 1 +		= 1 −		= 0 ⇔
	2 √ 72 − x2		√ 72 − x2

	x
⇔		= 1 ⇔ x = √ 72 − x2 ⇔ x2 = 72 − x2 ⇔ 2 x2 = 2*36 ⇔
	√72 − x2

⇔ x = 6 W punkcie x = 6 funkcja L ' zmienia znak z + na − , więc wtedy obwód L osiąga maksimum. Wtedy y = √72 − 6² = 6 A = ( 6, 0) B = ( 0 , 6) y = a x + b 0 = 6 a + b 6 = 0 + b ⇒ b = 6 −−−−− a = − 1 −−−−− Równanie prostej l : y = −x + 6 ==========

Razor3: Dziękuwa! Właśnie tak miałem, tylko myślałem, że jest jakieś inne prostsze rozwiązanie.