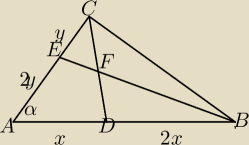
 W ΔABC z wierzchołka C poprowadzono odcinek na bok AB w taki sposób,że podzielił go na odcinki
w stosunku 1:2,analogicznie z wierzchołka B poprowadzono odcinek na bok AC dzieląc go również
w stosunku 1:2. Dany jest kąt CAB=α. Oblicz stosunek pola trójkąta ABC do pola czworokąta ADEF
W ΔABC z wierzchołka C poprowadzono odcinek na bok AB w taki sposób,że podzielił go na odcinki
w stosunku 1:2,analogicznie z wierzchołka B poprowadzono odcinek na bok AC dzieląc go również
w stosunku 1:2. Dany jest kąt CAB=α. Oblicz stosunek pola trójkąta ABC do pola czworokąta ADEF


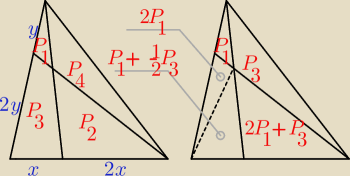 Szkic rozwiązania (bez komentarzy)
(pierwszy rysunek)
P1, P2, P3, P4 − pola figur
P = P1 + P2 + P3 + P4 to pole trójkąta ABC
P = 3(P1 + P3) = 3P1 + 3P3 (*) i P = 3(P1 + P4) = 3P1 + 3P4 ⇒ P4 = P3
2P1 + 2P3 = P2 + P4 ⇒ 2P1 + 2P3 = P2 + P3 ⇒ P2 = 2p1 + P3
−−−−−−−
(drugi rysunek)
Szkic rozwiązania (bez komentarzy)
(pierwszy rysunek)
P1, P2, P3, P4 − pola figur
P = P1 + P2 + P3 + P4 to pole trójkąta ABC
P = 3(P1 + P3) = 3P1 + 3P3 (*) i P = 3(P1 + P4) = 3P1 + 3P4 ⇒ P4 = P3
2P1 + 2P3 = P2 + P4 ⇒ 2P1 + 2P3 = P2 + P3 ⇒ P2 = 2p1 + P3
−−−−−−−
(drugi rysunek)
| 1 | 1 | 3 | |||
P = P1 + 2P1 + P1 + | P3 ⇒ P = 12P1 + | P3 (**) | |||
| 3 | 2 | 2 |
| 3 | ||
(*) i (**) ⇒ 3P1 + 3P2 = 12P1 + | P3 ⇒ P3 = 6P1 ⇒ P = 21P1} | |
| 2 |
| P | 21P1 | 7 | ||||
Odp.: | = | = |  | |||
| P3 | 6P1 | 2 |
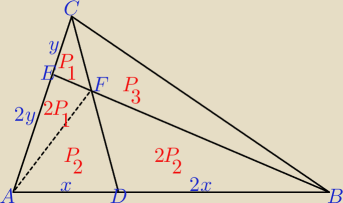 Jeszcze jedno spojrzenie na to zadanko: P1, P2, P3 − pola trójkątów.
2(P1 + 2P1 + P2) = 2P2 + P3 ⇒ P3 = 6P1
2(P1 + P3) = 2P1 + P2 + 2P2 ⇒ 14P1 = 2P1 + 3P2 ⇒ P2 = 4P1
Pole trójkąta ABC: P = P1 + 2P1 + P2 + 2P2 + P3 = 21P1
Pole czworokąta ADFE: 2P1 + P2 = 6P1
Jeszcze jedno spojrzenie na to zadanko: P1, P2, P3 − pola trójkątów.
2(P1 + 2P1 + P2) = 2P2 + P3 ⇒ P3 = 6P1
2(P1 + P3) = 2P1 + P2 + 2P2 ⇒ 14P1 = 2P1 + 3P2 ⇒ P2 = 4P1
Pole trójkąta ABC: P = P1 + 2P1 + P2 + 2P2 + P3 = 21P1
Pole czworokąta ADFE: 2P1 + P2 = 6P1