proszę o rozwiązanie
Michał: | | 1 | |
stożek o wysokości |
| *r gdzie r jest promieniem podstawy przecięto płaszczyznami
|
| | 3 | |
do których należy wierzchołek. Wyznacz ten przekrój którego pole jest największe i oblicz to
pole
nie wiem jaka to figura
16 lut 20:07
Bogdan:
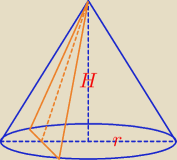
16 lut 20:12
Eve:
16 lut 20:12
Michał: czyli trzeba obliczyć pole trójkąta
16 lut 23:00
Michał: | | √10 | |
obliczyłem l = |
| − tworząca
|
| | 3 | |
przekrój jest trójkątem równoramiennym
16 lut 23:12
Michał: | | √10 | |
l = |
| *r zapomiałem o promieniu |
| | 3 | |
16 lut 23:18
Michał: czy ktoś ma pomysł
17 lut 16:59
Michał: ponawiam prośbę
| | 4 | |
dodatkowo obliczyłem kąt rozwarcia z tw cos i cos α = |
|
|
| | 5 | |
Dalej nie mam pomysłu
20 lut 08:35
J:
oznacz przez x odległość podstawy przekroju od środka okręgu ,
przez a połowę podstawy przekroju,
h wysokość przekroju , wtedy:
a =
√r2 − x2 i h =
√H2 + x2
| | 1 | |
P = |
| *2a*h = a*h = √r2 − x2*√H2 + x2
|
| | 2 | |
20 lut 08:56
Michał: J czy opierasz swój zapis według rysunku z 20 lut.20.12
20 lut 09:18
J:
tak
20 lut 09:35
Michał: muszę to rozpisać ale teraz muszę już wyjść dam odpowiedż póżniej
20 lut 09:46
Michał: jak obliczyć x
20 lut 16:40
Michał: czy ktoś ma pomysł na obliczenie długości odcinka x
20 lut 19:15
Michał: próbowałem z trójkątów podobnych ale nie otrzymałem takiego wyniku
21 lut 16:23
Michał: ponawiam prośbę jak obliczyć x
22 lut 16:57
Mila:
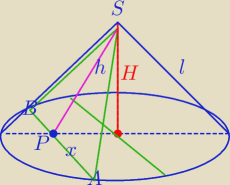
|AB|=2x
W ΔSPA:
l
2=x
2+h
2
h=
√10r29−x2
P
ABS(x)=x*
√10r29−x2
| | −2x | |
P'(x)=√10r29−x2+x* |
| ⇔ |
| | 2√10r29−x2 | |
| | −x2 | |
P'(x)=√10r29−x2+ |
| ⇔ |
| | √10r29−x2 | |
| | 10r29−2x2 | |
P'(x)= |
| |
| | √10r29−x2 | |
| | 10r2 | |
P'(x)=0⇔ |
| −2x2=0 i 0<x≤r |
| | 9 | |
| | r√5 | | 5r2 | |
PΔABS= |
| *√5r29= |
| |
| | 3 | | 9 | |
=================================
22 lut 17:30
Michał: dziękuję bardzo
ja też obliczyłem l i przy obliczaniu pochodnej robiłem dużo błędów
22 lut 17:56
Mila:
22 lut 17:57


 |AB|=2x
|AB|=2x