równania okręgu! gunia: PROSZĘ O SZYBKĄ POMOC! 1.do okręgu (x−7)² +(y+1)²=25 poprowadzono styczne z początku układu współrzędnych. Oblicz pole trójkąta którego wierzchołkami są punkty styczności oraz punkty przecięcia stycznych. 2. Napisz równanie okręgu przechodzącego przez punkt A=(2,2) oraz przez punkty przecięcia okręgu x²+y²−4x−4y−1=0 z prostą y+x=1 3.dane są punkty a=(−4 −2) b=(7 9) i c=(6 2). napisz równanie okręgu o środku w punkcie C stycznego do prostej AB 4.napisz równanie stycznych poprowadzonych z punktu p=(0.−5) do okręgu opisanego na trójkącie o wierzchołkach a=(4,2) b=(7,1) c=(6,−2) 5.okrąg którego środek leży na prostej 2x−y=0 jest styczny do prostych y=x+6 i y=−x+2 znajdź równanie tego okręgu.

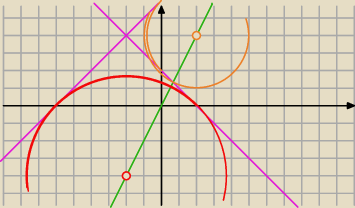
Tadeusz: 5) Środek okręgu S=(x, 2x) jest równoodległy od obu prostych

	|x−2x+6|		|−x−2x+2|
		=		⇒ |−x+6|=|−3x+2|
	√2		√2

−x+6=−3x+2 lub −x+6=3x−2 2x=−4 4x=8 x=−2 x=2 dalej już banał