Półkole z wpisanym protsokątem Lorien185: W dane półkole o promieniu r wpisano prostokąt o bokach a i b w taki sposób, że bok a leży na średnicy półkola. Przy jakiej wartości a/b pole prostokąta jest maksymalne? dzięki za pomoc! (jakąkolwiek...)

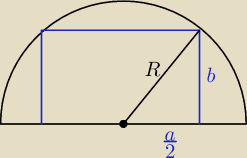
Qulka: a²/4+b² = R² P=ab=a(√R²−a²/4 i pochodna i =0 i znajdujesz a

J:

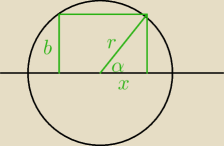
	x		b
P = 2x*b		= cosα ,		= sinα
	r		r

P = 2r²sinαcosα = r²sin2α ... ta funkcja ma maksimum dla 2α = 90⁰ , czyli dla α = 45

	a
stąd: x = b , czyli: a = 2x = 2b ⇔		= 2
	b

Lorien185: dzięki wielkie za pomoc!

Lorien185: Dobrze myślę, że pochodna wychodzi 2r²−a² / √4r²−a² Przyrównuję ją do 0 i ostatecznie mam że a=r √2 i a/b =2 ?

J: robiłaś/eś pierwszym sposobem , w moim wyszedł wynik taki sam

Lorien185: Musiałam robić pierwszym, bo drugiego mi na egzaminie nie uznają, gdyż w poleceniu jest słowo maksymalne co od razu narzuca nam pochodną....

J: przecież w moim sposobie też liczymy pochodną , tylko zmienną jest kat α P = r²sin2α P' = 2r²sin2αcos2α P' = 0 ⇔ cos2α = 0 ⇔ 2α = 90 ⇔ α = 45