powtóreczka :) Hajtowy: Powtórka do 2 semestru Wyznacz ekstrema oraz przedziały monotoniczności f(x) = x² * e^1/x Sprawdź czy podany schemat jest tautologią: [p⇒(q⇒r)] ⇔ [(p⋀q)⇒r]

J: f'(x) = e^1/x(2x − 1)

Hajtowy: I to tyle ? Wyznacz asymptoty funkcji:

	x3
f(x)=
	x2−1

Hajtowy: Tautologia nieaktualna, poradziłem sobie

J: ad 1) badasz znak pochodnej i ekstrema

J: wczesniej oczywiście dziedzina funkcji

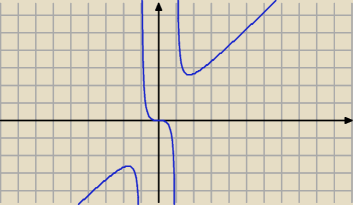
Qulka: asymptoty to liczysz granice w krańcach określoności czyli ±∞ ±1⁺⁻ będę 2 pionowe x=±1 i ukośna y=x

Hajtowy: Qulka możesz dokładniej to zrobić bo ja tego nie mialem a musze sie tego nauczyc

Hajtowy: Wyznacz ekstrema oraz przedziały monotoniczności f(x) = x² * e^1/x D_f=R ? f ' (x) = e^1/x(2x − 1) No i chyba teraz warunek konieczny do istnienia ekstremum ale jak?

J: D = R/{0} Kiedy pierwsza pochodna się zeruje ?

Hajtowy: Kiedy mianownik > 0 i e^1/x > 0 ; wteddy pochodna = 0

Qulka: Dziedzina : (−∞;−1) u (−1;1) u (1;∞) granice przy każdym nawiasie (bo to kraniec) więc:

	x3		x3		x
limx−>∞		=limx−>∞		=limx−>∞		=∞
	x2−1		x2(1−1/x2)		(1−1/x2)

	x3		x3		x
limx−>−∞		=limx−>−∞		=limx−>−∞
	x2−1		x2(1−1/x2)		(1−1/x2)

=−∞ granica w punkcie wstawiasz troszkę więcej (+) lub troszkę mniej (−) niż ten punkt i wykonujesz działamnia

	x3		−1
limx−>−1−		=limx−>−1−		= −∞
	x2−1		0+

	x3		−1
limx−>−1+		=limx−>−1+		= +∞
	x2−1		0−

	x3		1
limx−>1−		=limx−>1−		= −∞
	x2−1		0−

	x3		1
limx−>1+		=limx−>1+		= +∞
	x2−1		0+

skoro w nieskończonościach wyszła nieskończoność sprawdzasz czy jest ukośna y=ax+b

	f(x)		x3		x3
a= limx−>∞		= limx−>∞		= limx−>∞
	x		x(x2−1)		x3(1−1/x2)

	1
=limx−>∞		= 1
	(1−1/x2)

	x3		x3−x3+1
b=limx−>∞ f(x) −ax = limx−>∞		−x = limx−>∞
	(x2−1)		(x2−1)

	1
=limx−>∞		=0
	(x2−1)

J: równanie: f'(x) = 0 ⇔ e^1/x(2x − 1) = 0 ⇔ x = ?

Hajtowy: Dziękuję

Hajtowy: x=1/2